Алгебра: Задание 1: Разложить выражение на множители:

Задание 1:
Разложить выражение на множители:

Задание 1: Разложить выражение на множители:

Показать ответ

Ответ:

Настюша1лавруша

27.01.2022 05:50

1) (а-в)²=(в-а)²
Чтобы доказать тождество, нужно с тождественных преобразований:

либо правую часть привести к виду левой части;
либо левую часть привести к виду правой части ;
либо и левую и правую привести к какому другому одинаковому виду

Преобразуем левую часть:
(a - b)² = a² - 2ab + b²
Преобразуем правую часть:
(b-a)²=b² -2ba+a²

Так как аb=ba, то a²-2ab+b²=b²-2ba+a²
Значит
(a-b)²=(b-a)²

2) Выполняем тождественные преобразования левой части и приведем ее к виду правой части
(-a-b)²=(-a)²+2·(-a)·(-b)+(-b)²=a²+2ab+b²=(a+b)²

0,0(0 оценок)

Ответ:

prisyazhnasvet

09.10.2022 00:03

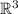Пусть $\varepsilon$ - канонический базис в $\mathbb{R}^{3}$ .

Тогда матрицу перехода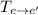 $T_{e \rightarrow e'}$ можно найти следующим образом:

$T_{e \rightarrow e'} = T_{e \rightarrow \varepsilon} \cdot T_{\varepsilon \rightarrow e'} = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

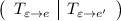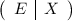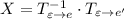
Если записать блочную матрицу $\left(\begin{array}{c|c}T_{\varepsilon \rightarrow e}&T_{\varepsilon \rightarrow e'}\end{array}\right)$ и привести путем элементарных преобразований к виду $\left(\begin{array}{c|c}E&X\end{array}\right)$ , то $X = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

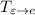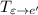Матрицу $T_{\varepsilon \rightarrow e}$ легко получить: достаточно записать в столбцы координаты векторов базиса . Аналогично с матрицей $T_{\varepsilon \rightarrow e'}$ .

В итоге необходимо получить вид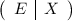 $\left(\begin{array}{c|c}E&X\end{array}\right)$ следующей матрицы:

$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\2&2&-1&5&8&1\\3&-3&2&-1&9&2\end{array}\right)$

Вычтем первую строку из второй и третьей:

$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\0&3&-2&0&1&0\\1&-2&1&-6&2&1\end{array}\right)$

Вычтем из первой строки 2 третьих и поменяем их местами:

$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&3&-1&17&3&-1\end{array}\right)$

Вычтем из третьей строки вторую:

$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&0&1&17&2&-1\end{array}\right)$

Прибавим ко второй строке 2 третьих и вычтем из первой третью:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&3&0&34&5&-2\\0&0&1&17&2&-1\end{array}\right)$

Делим вторую строку на 3:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

Прибавляем в первой строке 2 вторых:

$\left(\begin{array}{ccc|ccc}1&0&0&{-\frac{1}{3}}&\frac{10}{3}&\frac{2}{3}\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$