1)
Введём замену: .
Обратная замена:
2)
Введём замену:
По теореме Виета:
Мы не взяли 5, потому что оно не входит в область значений переменной . Обратная замена:
3)
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля.
Приравниваем числитель к нулю:
1)
Введём замену:![t = \cos x\ ,\ t\in [-1; 1]](/tpl/images/1574/9128/5cc33.png) .
.
Обратная замена:
2)
Введём замену:![t = \sin x\ ,\ t\in [-1; 1]](/tpl/images/1574/9128/dc10c.png)
По теореме Виета:
Мы не взяли 5, потому что оно не входит в область значений переменной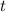 . Обратная замена:
. Обратная замена:
3)
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля.
Приравниваем числитель к нулю:
Введём замену: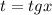 .
.
Обратная замена: