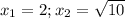Задано алгебраическое выражение: 3+54−2. Выберите значение , при котором это алгебраическое выражение принимает наибольшее значение среди перечисленных вариантов. =5
=2
=3
=1
=0

Пусть большее простое число из T(x) равно n.Сравним числа:n^2 и 2T(x),то есть квадрат наибольшего простого числа и удвоенную сумму простых чисел до n:

Очевидно,что все простые числа,кроме 2 нечетные,а значит T(x) меньше суммы двойки и натуральных нечетных чисел от 1 до n(так как не все нечетные числа являются простыми).

Рассмотрим данную сумму,члены которой,кроме двойки образуют арифметическую прогрессию.

Сравним 2S и n^2

Правая часть больше левой(нуля) при:

А так как S>T(X) и n^2>2S,то n^2>2T(x)

Значит и x^2>2T(x) при n,указанном выше.

Рассмотрим оставшиеся 2 варианта:

n=2 n=3

ответ: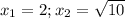

Пусть большее простое число из T(x) равно n.Сравним числа:n^2 и 2T(x),то есть квадрат наибольшего простого числа и удвоенную сумму простых чисел до n:

Очевидно,что все простые числа,кроме 2 нечетные,а значит T(x) меньше суммы двойки и натуральных нечетных чисел от 1 до n(так как не все нечетные числа являются простыми).

Рассмотрим данную сумму,члены которой,кроме двойки образуют арифметическую прогрессию.

Сравним 2S и n^2

Правая часть больше левой(нуля) при:

А так как S>T(X) и n^2>2S,то n^2>2T(x)

Значит и x^2>2T(x) при n,указанном выше.

Рассмотрим оставшиеся 2 варианта:

n=2 n=3

ответ: