По клеточкам можно определить: из прямоугольного равнобедренного треугольника его углы будут равны 45°, 45° и 90°.
Так как угол развёрнутый, то угол наклона будет равен 180° - 45° = 135°.
Следовательно Тут коэффициент показывает пересечение графика функции с осью ординат .
Из графика он равен 2.
Возьмём любую удобную точку из графика (кроме ):
Подставим их в формулу функции и получим:
ответ: -1.
По клеточкам можно определить: из прямоугольного равнобедренного треугольника его углы будут равны 45°, 45° и 90°.
Так как угол развёрнутый, то угол наклона будет равен 180° - 45° = 135°.
Следовательно Тут коэффициент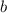 показывает пересечение графика функции с осью ординат
показывает пересечение графика функции с осью ординат 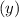 .
.
Из графика он равен 2.
Возьмём любую удобную точку из графика (кроме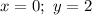 ):
):
Подставим их в формулу функции и получим:
ответ: -1.
для решения в целых числах необходимо, что бы подкоренное выражение было полным квадратом:
используем условие, что
второе условие системы выполняется всегда
получили:
ответ: (1+k;1-k;k); (1+k;1-k;-k); (1-k;1+k;k); (1-k;1+k;-k); где
Докажем, что
Пусть
тогда наше неравенство равносильно неравенству (его нам тепер нужно доказывать):
предлагаю разложить на множители уже самому
докажем, что
для это рассмотрим верное неравенство:
мы доказали, что
тогда
неравенство доказано