Задумали два числа. Если разность этих чисел умножить на 3, то получим число, большее суммы этих чисел на 9. Если разность задуманных чисел умножить на 2, то получим число, большее суммы этих чисел на 13. 1. Создай математическую модель по словесной.
Выбери все подходящие математические модели для решения задачи,
обозначив первое число за t, а второе за c:

{3(t−c)−t+c=9
2(t−c)−t+c=13

{3(t−c)−9=t+c
2(t−c)−13=t+c

{3+(t−c)=(t+c)+9
2+(t−c)=(t+c)+13

{3(t−c)=(t+c)+9
2(t−c)=(t+c)+13

{3(t−c)=(t+c)−9
2(t−c)=(t+c)−13

{3(t−c)−(t+c)=9
2(t−c)−(t+c)=13

{3(t−c)+9=t+c
2(t−c)+13=t+c

2. ответь на вопрос задачи.
Одно число равно
, а другое —
(первым пиши меньшее число).

Эта система немного сложнее и проще предыдущей.

Рассмотрим первое уравнение:

7y + 21x = 35  /7

y + 3x = 5

y = 5 - 3x

Мы выразили у, теперь подставим вместо него полученное выражение:

6x - 3xy = 54

6x - 3x (5-3x) = 54

Раскроем скобки:

6x - 15x + 9x² = 54

9x² - 9x - 54 = 0   /9

x² - x - 6 = 0

Теперь решим это квадратное уравнение (решу двумя : через дискриминант и через теорему Виета)

1. x² - x - 6 = 0

x₁ + x₂ = 1   |                                              x₁ = 3

                  |   по теореме Виета =>

x₁ * x₂ = -6  |                                              x₂ = -2

2. x² - x - 6 = 0

D = 1 + 24 = 25 (5²)

x₁ = (1 + 5) / 2 = 6/2 = 3

x₂ = (1 - 5) / 2 = -4 / 2 = -2

В этом пункте можно выбрать любой удобный решения. Итак, мы получили два х, а значит и у будет также два. Подставим оба значения х, чтобы найти значение у:

X₁.      y = 5 - 3x

         y = 5 - 3*3

         y = 5 - 9

         y = -4

X₂.     y = 5 - 3x

         y = 5 + 3*2

         y = 5 + 6

         y = 11

Таким образом у нас получилось две пары корней.

ответ: х₁ = 3; y₁ = -4 и x₂ = -2; y₂ = 11

Уравнение распадается на два. Рассмотрим первое уравнение:

Рассмотрим второе уравнение:

Заметим, что в левой и правой части стоят 11 степени некоторых выражений. Так как функция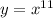 монотонно возрастает на всей области определения, то для этой функции можно сделать вывод: значения функций равны когда равны значения аргументов. Запишем:

Дорешаем это уравнение:

В соответствии с теоремой Виета:

Нетрудно заметить, что этим условиям удовлетворяют числа 1 и 5, но нас больше интересует именно их произведение:

Тогда, произведение всех корней:

ответ: -5