Записать свойства функции y=-3x² по схеме исследования свойств функции . 20 ​

Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.

Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.

1.

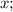
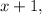
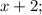
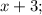
Пусть    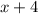          -  пять последовательных натуральных чисел, тогда их сумма равна:

Очевидно, что каждое слагаемое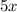  и 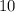   делится на 5, а это означает, что вся сумма делится на 5.

Доказано.

2.

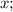
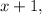
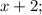
Пусть   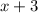       -  четыре последовательных натуральных числа, тогда их сумма равна:

Очевидно, что первое слагаемое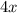  делится на 4, а второе слагаемое 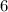не делится на 4, это означает, что вся сумма не делится на 4.

Доказано.

3.

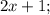
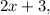
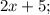
Пусть   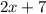          -  четыре последовательных нечётных натуральных числа, тогда их сумма равна:

Очевидно, что каждое слагаемое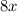  и 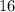   делится на 8, а это означает, что вся сумма делится на 8.

Доказано.

4.

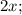
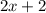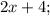
Пусть     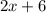 ;       -  четыре последовательных чётных натуральных числа, тогда их сумма равна:

Очевидно, что каждое слагаемое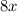  и 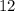   делится на 4, а это означает, что вся сумма делится на 4.

Доказано.

Чтобы определить количество корней в квадратном уравнении, достаточно вычислить его дискриминант по формуле: (если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена



Дискриминант больше нуля - два корня



Дискриминант равен нулю. В уравнении 1 корень



Дискриминант меньше нуля, значит нет действительных корней

2)

Найти область определения функции - это найти "проблемные точки" в функции, при которых функция перестанет существовать.
В нашем случае, это нельзя допускать, когда знаменатель обратится в ноль. Для этого мы должны его приравнять к нулю и выяснить, при каких значениях функция перестанет существовать.



В нашем случае функция не имеет смысла, при х=-1 и х=0