Запиши абсциссу и ординату точки A(7;−3). ответ:
абсцисса точки A
;
ордината точки A
.
Даны координаты точки. Определи, в какой координатной четверти находится данная точка.
Точка D(17;−18) находится в
.
3 четверти
2 четверти
1четверти
4четверти
Как расположены точки в координатной плоскости, если их ордината равна −4?
Расположены на прямой, параллельной оси y и пересекающей ось x в точке с этой ординатой
Расположены на прямой, параллельной оси x и пересекающей ось y в точке с этой ординатой
звестно, что точки A, B, C и D — вершины прямоугольника.
Дано: A(0;0);B(0;1);D(2;0).
Определи координаты четвёртой вершины C:
C(
;
).
Постарайся ответить, не выполняя построение на координатной плоскости!
1. Один конец отрезка находится в начальной точке координатной системы O(0;0).
Другой конец A имеет координаты (8;0).
Определи координаты серединной точки C отрезка OA.
C(
;
).
2. Один конец отрезка находится в начальной точке координатной системы O(0;0).
Другой конец B имеет координаты (0;16).
Определи координаты серединной точки D отрезка OB.
D(
;
).
3. Один конец отрезка находится в точке M с координатами (8;16), другой конец N имеет координаты (24;14).
Определи координаты серединной точки K отрезка MN.
K(
;
).
Пусть х - цифра десятков;
у - цифра единиц .
По условию цифра десятков, увеличенная на 2, в 2 раза больше цифры единиц.
Исходя из этого, получаем первое уравнение:
х +2 = 2у
Ещё в условии сказано, что если цифры десятков и единиц поменять местами, то полученное число будет меньше первоначального на 27, т.е.
(10х+у) > (10у+х) на 27
Получаем второе уравнение:
(10х+у ) - (10у+х) = 27
Упростим это уравнение:
9х - 9у = 27
х - у = 3
Решаем систему:
{x + 2 = 2y
{x - y = 3
Из второго уравнения выразим х:
х = у + 3
Подставим в первое:
у + 3 + 2 = 2у
у = 5 - цифра единиц
х = 5 + 3
х = 8 - цифра десятков;
ответ: 85
17
Объяснение:
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит,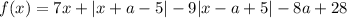
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
Наибольшее значение параметра — 17.