Найдём функцию Эйлера от числа 5. Это количество чисел, меньших 5 и взаимно простых с ним, то есть не имеющих с 5 общих делителей. Такими числами являются 1, 2, 3, 4, поскольку они не делятся на 5. Тогда функция Эйлера φ(5) = 4 (к тому же функция Эйлера простого числа, каким является 5, представляет собой результат вычитания единицы из этого числа, то есть 5 - 1 = 4, как у нас и получилось).
Так как 3 и 5 — взаимно простые числа, то сравнимо с 1 по модулю 5.
2020 = 5 * 404
Тогда можно записать в виде
Поскольку мы выяснили, что сравнимо с 1 по модулю 5, то также сравнимо с 1 по модулю 5. То есть остаток равен 1.
ответ:Формула:
sin α ·cos β –cos α ·sin β =sin( α – β )
sin(x–(π/4))=√3/2
Уравнение: sint=√3/2 – простейшее тригонометрическое уравнение решают по формулам: t=(–1)karcsin(√3/2)+πk, k ∈ Z
х–(π/4)=(–1)karcsin(√3/2)+πk, k ∈ Z
х–(π/4)=(–1)k·(π/3)+πk, k ∈ Z
х=(–1)k·(π/3)+(π/4)+πk, k ∈ Z – это ответ.
Так как (–1)k·(π/3)+πk, k ∈ Z можно записать в виде серии из двух ответов:
k=2n
(π/3)+2πn, n ∈ Z
k=2n+1
(2π/3)+2πn, n ∈ Z
то ответ можно записать и так.
х=(π/3)+(π/4)+2πn=(7π/12)+2πn, n ∈ Z или
х=(2π/3)+(π/4)+2πn=(11π/12)+2πn, n ∈ Z
Такая запись полезна при отборе корней
Объяснение:
1
Объяснение:
Найдём функцию Эйлера от числа 5. Это количество чисел, меньших 5 и взаимно простых с ним, то есть не имеющих с 5 общих делителей. Такими числами являются 1, 2, 3, 4, поскольку они не делятся на 5. Тогда функция Эйлера φ(5) = 4 (к тому же функция Эйлера простого числа, каким является 5, представляет собой результат вычитания единицы из этого числа, то есть 5 - 1 = 4, как у нас и получилось).
Так как 3 и 5 — взаимно простые числа, то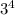
сравнимо с 1 по модулю 5.
2020 = 5 * 404
Тогда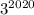
можно записать в виде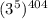 
Поскольку мы выяснили, что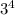
сравнимо с 1 по модулю 5, то 
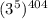также сравнимо с 1 по модулю 5. То есть остаток равен 1.