Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина? часов. А легковая, соответственно, часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на часа раньше, значит, в целом она пробыла в пути на часов меньше.
- разница во времени.
Составим уравнение:
.
Избавимся от знаменателей, умножив обе части на общий множитель 3х.
Найдем простую радикальную форму данного в задании корня, для этого умножим его на сопряженное число: 1/(6+√2) * (6-√2) / (6-√2) = (6-√2) / (6-√2)(6+√2) =(6-√2) / (36-2) = (6-√2)/34
если наше уравнение ax^2 + bx + c =0 должно быть c рац. коэфф., то кв. корень из дискриминанта должен быть кратен √2(иначе кв. корню неоткуда взяться), откуда (и из формулы корней кв. ур-я) следует, что второй корень уравнения должен быть (6+√2)/34
пусть a = 1, тогда согласно теореме Виетта (6+√2)/34 * (6-√2)/34 = с (6+√2)/34 + (6-√2)/34 = -b
c = (36-2)/(34*34) = 1/34 b = -12/34 = -6/17
и наше уравнение x^2 -6/17x + 1/34 = 0 ну или в более человеческом виде (умножаем обе части на 34) 34x^2 - 12x + 1 =0
Скорость грузовой машины - 40км/ч.
Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина?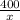
часов. А легковая, соответственно, 
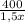часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на 
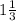часа раньше, значит, в целом она пробыла в пути на 
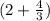часов меньше.
Составим уравнение:
Избавимся от знаменателей, умножив обе части на общий множитель 3х.
Получим: 800 = 1200 - 10х
10х=400
х=40.
А это и есть скорость грузовика
1/(6+√2) * (6-√2) / (6-√2) = (6-√2) / (6-√2)(6+√2) =(6-√2) / (36-2) = (6-√2)/34
если наше уравнение ax^2 + bx + c =0 должно быть c рац. коэфф., то кв. корень из дискриминанта должен быть кратен √2(иначе кв. корню неоткуда взяться), откуда (и из формулы корней кв. ур-я) следует, что второй корень уравнения должен быть (6+√2)/34
пусть a = 1, тогда согласно теореме Виетта
(6+√2)/34 * (6-√2)/34 = с
(6+√2)/34 + (6-√2)/34 = -b
c = (36-2)/(34*34) = 1/34
b = -12/34 = -6/17
и наше уравнение
x^2 -6/17x + 1/34 = 0
ну или в более человеческом виде (умножаем обе части на 34)
34x^2 - 12x + 1 =0