Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t) - объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит, - цис./ч - производительность "медленного" насоса.
Тогда - цис./ч - производительность "быстрого" насоса.
Следовательно, ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
(a²+4)/(4a)
Объяснение:
Как бестолково написано: (2-a/2+a-a+2/a-2):(2+a/2-a+a-2/a+2).
Может всё-таки так?
((2-a)/(2+a) -(a+2)/(a-2))÷((2+a)/(2-a) +(a-2)/(a+2))=(a²+4)/(4a)
1) (2-a)/(2+a) -(a+2)/(a-2)=(2-a)/(2+a) +(a+2)/(2-a)=((a-2)²+(a+2)²)/(4-a²)
2)(2+a)/(2-a) +(a-2)/(a+2)=(a-2)/(a+2) -(2+a)/(a-2)=((a-2)²-(a+2)²)/(a²-4)
3) ((a-2)²+(a+2)²)/(4-a²) ÷((a-2)²-(a+2)²)/(a²-4)=-((a-2)²+(a+2)²)/(a²-4) ·(a²-4)/((a-2)²-(a+2)²)=-(a²-4a+4+a²+4a+4)/((a-2-a-2)(a-2+a+2))=-(2a²+8)/(-4·2a)=(-2(a²+4))/(-4·2a)=(a²+4)/(4a)
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)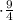
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: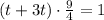
9t = 1
Значит,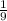
- цис./ч - производительность "медленного" насоса.
Тогда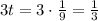
- цис./ч - производительность "быстрого" насоса.
Следовательно,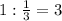
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
(a²+4)/(4a)
Объяснение:
Как бестолково написано: (2-a/2+a-a+2/a-2):(2+a/2-a+a-2/a+2).
Может всё-таки так?
((2-a)/(2+a) -(a+2)/(a-2))÷((2+a)/(2-a) +(a-2)/(a+2))=(a²+4)/(4a)
1) (2-a)/(2+a) -(a+2)/(a-2)=(2-a)/(2+a) +(a+2)/(2-a)=((a-2)²+(a+2)²)/(4-a²)
2)(2+a)/(2-a) +(a-2)/(a+2)=(a-2)/(a+2) -(2+a)/(a-2)=((a-2)²-(a+2)²)/(a²-4)
3) ((a-2)²+(a+2)²)/(4-a²) ÷((a-2)²-(a+2)²)/(a²-4)=-((a-2)²+(a+2)²)/(a²-4) ·(a²-4)/((a-2)²-(a+2)²)=-(a²-4a+4+a²+4a+4)/((a-2-a-2)(a-2+a+2))=-(2a²+8)/(-4·2a)=(-2(a²+4))/(-4·2a)=(a²+4)/(4a)