Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
Nigira
04.06.2021 09:02 •
Алгебра
Запишите выражение для нахождения суммы первых n членов прогрессии (bn) если : а)b1=1,q=5; б)b1=1,q=1/3 ' решить '
Показать ответ
Ответ:
malina78911
11.06.2020 23:27
Сумма первых n членов геометрической прогрессии:
a)
б)
0,0
(0 оценок)
Популярные вопросы: Алгебра
Werevolk1
01.10.2020 06:34
Сначала всего пути а потом 25% остатка. сколько % всего пути осталось пройти?...
zhanik2017
01.10.2020 06:34
36 ! решите системой х+у =8 2х-у=7...
bilyikot
01.10.2020 06:34
Решите : 1) (4x-3)²-6x(4-x). 2) (p+3)(p-11)+(p+6)². 3) (a-x)²+(a+x)². 4) 2(x+6)²-(20x+70)...
moskaliov
01.10.2020 06:34
Изобразите схематически график функции y=-5(2-|x|)^1/2...
Асия22222
01.10.2020 06:34
С( нужно составить уравнение): путь от пункта а до пункта в поезд преодолел за 3 часа. за первый час он проехал 30% всего пути, за второй час 5/6 пути, пройденного за первый час,...
markmordachev
01.10.2020 06:34
Числитель 2у²+7у+3 знаменатель у²-9...
приветЯ11
10.03.2023 17:22
Николаю надо было добраться из дома на дачу.половину пути он преодолел на автобусе, двигавшемся с постоянной скоростью, а оставшуюся часть - пешком со скоростью в 5 раз меньше....
KrasnovaLu82
10.03.2023 17:22
Разложите на множители многочлены 2ху^2 - 18х...
kisa1756
10.03.2023 17:22
Разложите многочлен на множители : 4а^2b^6+20ab^3c+25c^2 ,!...
HomelessGod1
24.01.2022 03:52
Постройте график функции и укажите промежутки ее возрастания, убывания: y=3x^2-6x+1...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Сумма первых n членов геометрической прогрессии: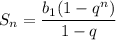
a)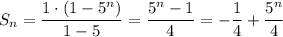
б)