1) x = ±
2) y =±
3) z = ±
4) k = ±
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
y^2 = 3
y = ±
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 =
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
z^2 = 3
z = ±
4) x^4 - 10x^2 + 9 = 0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
k^2 = 2
k = ±
6) 49y^4 - 48y^2 - 1 = 0
49t^2 - 48t - 1 = 0
t2 = -1 - посторонний
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
x1 = 1
x2 = 4
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5
y
=
6
x
−
2
Переставим
и
.
+
Определим свойства данной параболы.
Нажмите, чтобы увидеть больше шагов...
Направление: направлено вниз
Вершина:
(
3
,
9
)
Фокус:
35
4
Ось симметрии:
Направляющая:
37
Выберем несколько значений
и подставим их в уравнение, чтобы найти соответствующие значения
. Значения
должны выбираться близко к вершине.
1
5
8
Построим график параболы, используя ее свойства и выбранные точки.
1) x = ±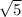
2) y =±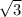
3) z = ±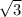
4) k = ±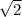
5) x1 = ±1; x2 = ±3
6) y = ±1
7)t1 = ±1; t2 = ±2
8)x1 = ±3; x2 = ±0.5
Объяснение:
1) x^4 - x^2 - 20 = 0
Замена x^2 = t >0
t^2 - t - 20 = 0
D = 1 + 4*20 = 81 = 9^2
t1 = (1 + 9)/2 = 5
t2 = (1 - 9)/2 = -4 - посторонний
Обратная замена
x^2 = 5
x = ±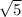
2)y^4 - 6y^2 + 9 = 0
Замена y^2 = t >0
t^2 - 6t + 9 = 0
D = 36 - 4*9 = 0
t = (6 ± 0)/2 = 3
Обратная замена
y^2 = 3
y = ±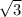
3) z^4 - z^2 - 6 = 0
Замена z^2 = t >0
t^2 - t - 6 = 0
D = 1 + 4*6 = 25 =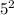
t1 = (1 + 5)/2 = 3
t2 = (1 - 5)/2 = -2 - посторонний
Обратная замена
z^2 = 3
z = ±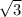
4) x^4 - 10x^2 + 9 = 0
Замена x^2 = t >0
t^2 - 10t + 9 = 0
т.к. a + b + c = 0
t1 = 1
t2 = 9
Обратная замена
x^2 = 1 или x^2 = 9
x1 = ±1
x2 = ±3
4) k^4 + 5k - 14 = 0
Замена k^2 = t >0
t^2 + 5t - 14 = 0
D = 25 + 4*14 = 81
t1 = (-5 + 9)/2 = 2
t2 = (-5 - 9)/2 = -7 - посторонний
Обратная замена
k^2 = 2
k = ±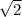
6) 49y^4 - 48y^2 - 1 = 0
Замена y^2 = t >0
49t^2 - 48t - 1 = 0
т.к. a + b + c = 0
t1 = 1
t2 = -1 - посторонний
Обратная замена
y^2 = 1
y = ±1
7) t^4 - 5t^2 + 4 = 0
Замена t^2 = x >0
x^2 - 5x + 4 = 0
т.к. a + b + c = 0
x1 = 1
x2 = 4
Обратная замена
t^2 = 1 или t^2 = 4
t1 = ±1
t2 = ±2
8) 4x^4 - 37x + 9 = 0
Замена x^2 = t >0
4t^2 - 37t + 9 = 0
D = 1369 - 4*4*9 = 35²
t1 = (37 + 35)/8 = 9
t2 = (37 - 35)/8 = 0.25
Обратная замена
x^2 = 9 или x^2 = 0.25
x1 = ±3
x2 = ±0.5
y
=
6
x
−
x
2
Переставим
6
x
и
−
x
2
.
y
=
−
x
2
+
6
x
Определим свойства данной параболы.
Нажмите, чтобы увидеть больше шагов...
Направление: направлено вниз
Вершина:
(
3
,
9
)
Фокус:
(
3
,
35
4
)
.
Ось симметрии:
x
=
3
Направляющая:
y
=
37
4
Выберем несколько значений
x
и подставим их в уравнение, чтобы найти соответствующие значения
y
. Значения
x
должны выбираться близко к вершине.
Нажмите, чтобы увидеть больше шагов...
x
y
1
5
2
8
3
9
4
8
5
5
Построим график параболы, используя ее свойства и выбранные точки.
Направление: направлено вниз
Вершина:
(
3
,
9
)
Фокус:
(
3
,
35
4
)
.
Ось симметрии:
x
=
3
Направляющая:
y
=
37
4
x
y
1
5
2
8
3
9
4
8
5
5