Пересечение- это то, что у них общее, а объединение- это всё, что есть в обоих множествах(но без повторений одного и того же)
а)A={простые числа, не превосходящих 40}
B={двузначные числа}
A∩B={11,13,17,19,23,29,31,37}
A∪B={все простые числа, не превосходящих 40(2,3,5,7,11,13,17,19,23,29,31,37)+все двузначные числа(т.е. от 10 до 99, но не повторяясь с теми, которые уже есть)}
б)A={натуральные, кратные 19}
B={двузначные числа}
A∩B={19,38,57,76,95}
A∪B={все двузначные числа+ числа, кратные 19(но уже те, которые после 100, чтобы не повторяться)}
а) A(n) = 2 - 3 · n;
A(1) = -1
A(2) = -4
A(3) = -7
A(4) = -10
A(5) = -13
б) A(n) = 50 - 7 · n;
A(1) = 43
A(2) = 36
A(3) = 29
A(4) = 22
A(5) = 15
в) B(n) = 1 ÷ n + 1;
B(1) = 2
B(2) = 1,5
B(3) =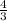
B(4) = 1,25
B(5) = 1,2
г) B(n) = n³
B(1) = 1
B(2) = 8
B(3) = 27
B(4) = 64
B(5) = 125
Объяснение:
а) A(n) = 2 - 3 · n;
A(1) = 2 - 3 · 1 = -1
A(2) = 2 - 3 · 2 = -4
A(3) = 2 - 3 · 3 = -7
A(4) = 2 - 3 · 4 = -10
A(5) = 2 - 3 · 5 = -13
б) A(n) = 50 - 7 · n;
A(1) = 50 - 7 · 1 = 43
A(2) = 50 - 7 · 2 = 36
A(3) = 50 - 7 · 3 = 29
A(4) = 50 - 7 · 4 = 22
A(5) = 50 - 7 · 5 = 15
в) B(n) = 1 ÷ n + 1;
B(1) = 1 ÷ 1 + 1 = 2
B(2) = 1 ÷ 2 + 1 = 1,5
B(3) = 1 ÷ 3 + 1 =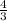
B(4) = 1 ÷ 4 + 1 = 1,25
B(5) = 1 ÷ 5 + 1 = 1,2
г) B(n) = n³
B(1) = 1³ = 1
B(2) = 2³ = 8
B(3) = 3³ = 27
B(4) = 4³ = 64
B(5) = 5³ = 125
Пересечение- это то, что у них общее, а объединение- это всё, что есть в обоих множествах(но без повторений одного и того же)
а)A={простые числа, не превосходящих 40}
B={двузначные числа}
A∩B={11,13,17,19,23,29,31,37}
A∪B={все простые числа, не превосходящих 40(2,3,5,7,11,13,17,19,23,29,31,37)+все двузначные числа(т.е. от 10 до 99, но не повторяясь с теми, которые уже есть)}
б)A={натуральные, кратные 19}
B={двузначные числа}
A∩B={19,38,57,76,95}
A∪B={все двузначные числа+ числа, кратные 19(но уже те, которые после 100, чтобы не повторяться)}