Метод интервалов – простой решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной. Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения .
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : .
Метод интервалов позволяет решить его за пару минут.В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.Метод интервалов основан на следующем свойстве дробно-рациональной функции.Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида . Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.Эти точки разбивают ось на N промежутков.Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
1) Решение через дискриминант .
2) Решение с выделения полного квадрата .
3) Решение с теоремы Виета.
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения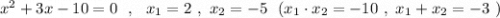 .
.
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения :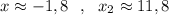 .
.