Алгебра: Здравствуйте Хоть один пример

Здравствуйте Хоть один пример

Показать ответ

Ответ:

Камила15111

25.05.2023 15:19

Поскольку график данной функции проходит через точку М(3; -1/11), то имеем: -1/11 = 1/(-9 + 3а - 4); -1/11 = 1/(-13 + 3а); -13 + 3а = -11; 3а = 2; а = 2/3.

у = 1/(-х² + (2/3)х - 4)

Наименьшее значение этой функции совпадает с наибольшим значением функции f(x) = -х² + (2/3)х - 4 (наибольшим значением знаменателя), которое равно значению ординаты вершины прараболы f(x) = -х² + (2/3)х - 4.

х₀ = -b/(2a) = -(2/3)/(-2) = 1/3 - абсциса вершины, f(1/3) = -1/9 + 2/9 - 4 = -35/9 - ордината вершины.

Значит y = 1/(-35/9) = -9/35 - наименьшее значение данной функции.

ответ: -9/35.

0,0(0 оценок)

Ответ:

ирка137

10.05.2021 12:01

За интеграл я буду Июиспользовать вот этот знак:

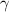
$\gamma$

4 пример:

1) Перепишите дробь:

$\gamma - \frac{1}{x} + \frac{2}{x + 6} dx$

2) Использовать свойства интегралов:

$- \gamma \frac{1}{x} dx + \gamma \frac{2}{x + 6} dx$

3) Вычислить интегралы и прибавить константу интегрирования С:

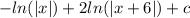
- ln( |x| ) + 2 ln( |x + 6| ) + c

5 пример:

1) Найти неопределённый интеграл:

$\gamma x \sqrt{x + 8} dx$

2) Упростить интеграл, используя метод замены переменной:

$\gamma t \sqrt{t} - 8 \sqrt{t} dt$

3) Преобразовать выражения:

$\gamma t \times {t}^{ \frac{1}{2} } - 8 {t}^{ \frac{1}{2} } dt$

4) Вычислить произведение:

$\gamma {t}^{ \frac{3}{2} } - 8 {t}^{ \frac{1}{2} } dt$

5) Использовать свойство интегралов:

$\gamma {t}^{ \frac{3}{2} } dt - \gamma 8 {t}^{ \frac{1}{2} } dt$

6) Вычислить интегралы:

$\frac{2 {t}^{2} \sqrt{t} }{5} - \frac{16t \sqrt{t} }{3}$

7) Выполнить обратную замену:

$\frac{2 {(x + 8)}^{2} \times \sqrt{x + 8} }{5} - \frac{16(x + 8) \sqrt{x + 8} }{3}$

8) Упростить выражение:

$\frac{2 \sqrt{x + 8} \times ( {x}^{2} + 16x + 64) }{5} - \frac{16(x + 8) \sqrt{x + 8} }{3}$

9) Вернуть пределы интегрирования и подставить в пример (8):

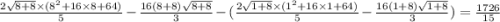
$\frac{2 \sqrt{8 + 8} \times ( {8}^{2} + 16 \times 8 + 64) }{5} - \frac{16(8 + 8) \sqrt{8 + 8} }{3} - ( \frac{2 \sqrt{1 + 8} \times ( {1}^{2} + 16 \times 1 + 64)}{5} - \frac{16(1 + 8) \sqrt{1 + 8} }{3} ) = \frac{1726}{15}$

6 пример