Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .
Рассмотрим многочлен , где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :
- степень определяется выражением , то есть степень равна 84
- свободный член равен
- степень определяется выражением , то есть степень равна 6
Наконец, для многочлена получим:
- степень определяется выражением , то есть степень равна 90
Сумма степени и свободного члена многочлена :
ответ: 98
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение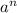 .
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение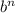 .
.
Рассмотрим многочлен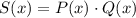 , где:
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена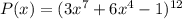 :
:
- степень определяется выражением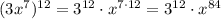 , то есть степень равна 84
, то есть степень равна 84
- свободный член равен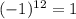
Для многочлена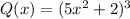 :
:
- степень определяется выражением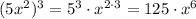 , то есть степень равна 6
, то есть степень равна 6
- свободный член равен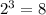
Наконец, для многочлена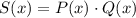 получим:
получим:
- степень определяется выражением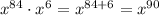 , то есть степень равна 90
, то есть степень равна 90
- свободный член равен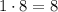
Сумма степени и свободного члена многочлена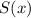 :
:
ответ: 98
cos(π/2-3x)= cos (3x-π/2)
Решаем уравнение:
cos ( 3x-π/2) = √3/2
3x - π/2 = ± arccos (√3/2) + 2π·n, n∈ Z
3x - π/2 = ± (π/6) + 2π·n, n∈ Z
3x = π/2 ± (π/6) + 2π·n, n∈ Z
x = π/6 ± (π/12) + (2π/3)·n, n∈ Z
или
вычитая получим: складывая получим:
х₁= π/2 - (π/6) + (2π/3)·n, n∈ Z х₂= π/2 + (π/6) + (2π/3)·n, n∈ Z
х₁= π/3 + (2π/3)·n, n∈ Z х₂=2π/3 + (2π/3)·n, n∈ Z
при n =0 получаем корни
π/3 и 2π/3
при n = 1
(π/3) + (2π\3) = π и (2π/3) + (2π/3)= 4π/3
при n = 2
(π/3) + (2π/3)·2=(5π\3) и ( 2π/3) +(2π/3)·2=(6π\3)=2π
3π/2 <(5π/3) <2π
3π/2 < 2π≤2π
ответ. На [3π/2; 2π] два корня: (5π.3) и 2π