(желательно с объяснением) 1. Даны концы отрезков AB: A (-4;2) и B (10;6). Точка M - середина AB. Найти длину OM.

2. Найти точку пересечения прямых 2x+4y-4z-6=0 и x+2y-2z+9=0.

3. Координаты вершин треугольника ABC : A(2;1) В(-1;4) и С(3; -2). Найти угол ABC.

Відповідь: а) (а-3)(а+3)=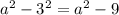                                                                   б) (a-5)(a+5)= 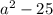                                                                                                   в) (8+a)(8-a)=64- 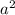                                                                                                              г) (a-14)(14+a)=(a-14)(a+14)= 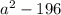                                                                                       д) (4a-2)(4a+2)= 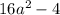                                                                                               е) 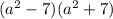= 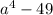                                                                                                   ж) (6a-8b)(6a+8b)=

Пояснення:

Дано неравенство: 6x² − x - 5 > 0.

Находим корни квадратного трёхчлена: 6x² − x - 5 = 0.

Квадратное уравнение, решаем относительно x:

Ищем дискриминант:

D=(-1)^2-4*6*(-5)=1-4*6*(-5)=1-24*(-5)=1-(-24*5)=1-(-120)=1+120=121;

Дискриминант больше 0, уравнение имеет 2 корня:

x1=(√121-(-1))/(2*6)=(11-(-1))/(2*6)=(11+1)/(2*6)=12/(2*6)=12/12=1;

x2=(-√121-(-1))/(2*6)=(-11-(-1))/(2*6)=(-11+1)/(2*6)=-10/(2*6)=-10/12=-(5/6)≈-0.833333.

откуда x1 = 1 и x2 = -(5/6).

Раскладываем левую часть неравенства на множители: 6(x – 1) (x +(5/6)) > 0. Точки -5/6 и 1 разбивают ось X на три промежутка:

ОО⟶Х

-5/6 1

Точки -5/6 и 1 выколоты. Это связано с тем, что решаемое неравенство — строгое (так что x не может равняться -5/6 или 1). Далее определяем знаки левой части неравенства на каждом из промежутков

+ – +

ОО⟶Х

-5/6 1

Получаем: x < -5/6 или x > 1.