Желательно в тетради надо сделать

Двухзначное число больше удвоенного произведения его цифр на 5, а от удвоенной суммы цифр - на 3. Найдите эти число.

Решение.

Пусть x - цифра десятков данного числа;

         y - цифра единиц этого числа

тогда

(10x+у) - данное двухзначное число.

ОДЗ: х∈N; 1≤x≤9;

         y∈N; 0≤y≤9

По условию  10х+у > 2·(x·y) на 5.

Получаем первое уравнение:

10x+у - 2xy = 5

И ещё по условию  10х+у > 2·(x+y) на 3.

Получаем второе уравнение:

10x+у - 2·(x+y) = 3

Упростим его:

10x+у-2x-2y = 3

8х - у = 3

Решаем систему:

∉N

y=8x-3 при x=1

y=8·1-3

y=5

        1- цифра десятков данного числа;

        5 - цифра единиц этого числа

ответ: 15.

Объяснение:

Рассмотрим сначала первое неравенство системы.

Начнем с ОДЗ:

Продолжим решение:

1)

Замена: .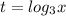

Обратная замена:

С учетом ОДЗ оба корня подходят.

2)

С учетом ОДЗ получим, что решение неравенства:

Теперь перейдем ко второму неравенству системы:

Понятно, что сначала нужно написать ОДЗ.

Продолжим решение:

Заметим, что данное неравенство хорошо раскладывается на множители:

Решим неравенство по методу интервалов.

1)

2)

Введем функци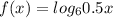и и 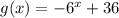. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 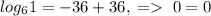, верно. Так, мы решили это уравнение, получив, что его корень x=2.

Тогда решение неравенства с учетом ОДЗ:

Итого имеем:

Найдем пересечение:

Задание выполнено!