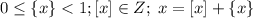Алгебра: Зная, что 5,1 х 6,3 и 2 у 2,4 оцените 1) ху; 2) -3х + у

Зная, что 5,1 < х < 6,3 и 2 < у < 2,4 оцените
1) ху;
2) -3х + у

Зная, что 5,1 < х < 6,3 и 2 < у < 2,4 оцените 1) ху; 2) -3х + у

Показать ответ

Ответ:

ПолинаПять

25.10.2020 09:33

Много избыточных данных в . видимо чтобы запутать. мне представляется все гораздо проще. если скорость каждого автобуса увеличится в двое, то в двое увеличится и их общая скорость сближения, следовательно в двое уменьшиться время в пути. значит и к месту встречи они доберутся в двое быстрее. и встретятся а во сколько они выехали? мы не знаем их время в пусть выехали они в 6 утра. встретились в 12 дня. в пути были 12-6=6 часов. увеличив в двое скорость - в двое уменьшится скорость в пути 6: 2=3 ч. встретятся они в 6+3=9 ч. или еще как вариант, но не уверен в правильности обозначим скорости автобусов через х и у, тогда х+у в 12.00 2х+у в 12.00 - 0.56 = 11.04 х+2у в 12.00 - 1.05 = 10.55 если сложим два последних уравнения (2х+у)+(х+2у) и вычтем первое (2х+у)+(х++у)=2х+у+х+2у-х-у=2х+2у а теперь попробуем тоже самое сделать с правыми частями 11.04+10.55-12.00=21.59 - 12.00= 9.59 получается так, что встреча будет в 9.59

0,0(0 оценок)

Ответ:

AnastasiyaSm

06.02.2020 17:04

По определению,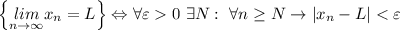 $\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение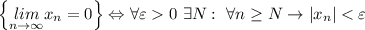 $\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

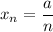
2) $x_n=\dfrac{a}{n}$

|x_n|

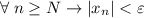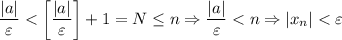
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

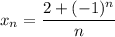
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1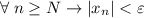$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда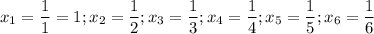 $x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$