Будем решать уравнение как квадратное относительно...
Допустим, относительно х. То есть представим себе, что х - переменная, а у - какое-то число, как 2,-1 и т.д. И оперировать будем с у, как с обычным числом, то есть в квадратном уравнении он будет участвовать в формировании коэффициентов a,b,c. Приведем уравнение к красивому виду.
Дискриминант получился полным квадратом, естественно, не случайно. В таких заданиях обычно (но не всегда) дают линейные зависимости, которые мы чуть позже получим.
Чтобы построить график уравнения, нужно выразить y через x. Со вторым иксом нам повезло, выражать ничего не надо, да и в первом не сильно сложно
То есть имеем
Соответственно, решением уравнения является объединение множеств точек, задаваемых этими двумя зависимостями.
График будет приложен.
А теперь ради интереса проделаем все то же самое, но относительно y (умножим уравнение на -1)
Получили то же самое, чего и следовало ожидать.
А вообще, это лишь частный случай и, по идее, тут и простым разложением на множители можно это сделать.
А вообще, это гораздо более общая задача, если уж обратиться к аналитической геометрии. Так как есть общее уравнение линии второго порядка
Есть теорема о приведении уравнения такого вида к одному из 9 канонических случаев. Это может быть: 1) эллипс, 2) гипербола, 3) парабола, 4) мнимый эллипс, 5) пара пересекающихся прямых, 6) пара мнимых пересекающихся прямых, 7) пара параллельных прямых, 8) пара мнимых параллельных прямых, 9) пара совпавших прямых.
Вот их уравнения по порядку. Причем это в новой системе координат, которая является результатом аффинных преобразований - поворота и переноса исходной системы координат. Если не углубляться в квадратичные формы, то нужно уметь считать определители и решать простенькие системы уравнений и немного знать тригонометрию. Координаты, угол и вид через большое количество действий вычисляются.
Если же идти через квадратичные формы, то там уже надо знать линейную алгебру (помимо определителей, обратных матриц, надо знать, как составлять матрицу квадратичной формы, знать про собственные вектора матрицы, уметь делать переходы к новому базису и т.д. и сделать можно в итоге через метод Лагранжа, а можно и через ортогональное преобразование).
То есть данная задача хороша на применение различных методов, которые были в свое время разработаны.
(P.S. цвета на графике разные, потому что просто хотел показать, где какая прямая, так как объединение множеств, то должно быть, по-хорошему, одного цвета)
В вопросе наверно опечаточка.
f(x) = - 4*x² + 4*x - 1
Объяснение:
Дано: y =-4*x²+4*x - 1 - квадратное уравнение.
Пошаговое объяснение:
1) Область определения - непрерывная, гладкая.
D(f) = R - ООФ - ответ.
D(f) = (-∞;+∞) - другая запись.
2) Пересечение с осью ОХ.
a*x² + b*x + c = 0
Вычисляем дискриминант - D.
D = b² - 4*a*c = 4² - 4*(-4)*(-1) = 0 - дискриминант. √D = 0.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (-4+0)/(2*-4) = -4/-8 = 0,5 - первый корень
x₂ = (-b-√D)/(2*a) = (-4-0)/(2*-4) = -4/-8 = 0,5 - второй корень
0,5 - точка пересечения с осью ОХ.
3) У(0) = - 1 - точка пересечения с осью ОУ.
4) Функция общего вида - ни чётная ни нечётная.
5) Поиск экстремума по первой производной.
f'(x) = 8*x + 4 = 4*(2*x + 1) = 0
x = 0.5 - точка экстремума
6) Локальный экстремум.
y(0.5) = 0 - максимум.
7) Возрастает: х= (-∞;0,5), убывает: х= (0,5;+∞)
8) Поиск точки перегиба по второй производной.
f"(x) = 8.
Корней нет и точек перегиба нет.
8) Выпуклая во всей ООФ.
Построение графика по точкам - в приложении.
Будем решать уравнение как квадратное относительно...
Допустим, относительно х. То есть представим себе, что х - переменная, а у - какое-то число, как 2,-1 и т.д. И оперировать будем с у, как с обычным числом, то есть в квадратном уравнении он будет участвовать в формировании коэффициентов a,b,c. Приведем уравнение к красивому виду.
Дискриминант получился полным квадратом, естественно, не случайно. В таких заданиях обычно (но не всегда) дают линейные зависимости, которые мы чуть позже получим.
Чтобы построить график уравнения, нужно выразить y через x. Со вторым иксом нам повезло, выражать ничего не надо, да и в первом не сильно сложно
То есть имеем
Соответственно, решением уравнения является объединение множеств точек, задаваемых этими двумя зависимостями.
График будет приложен.
А теперь ради интереса проделаем все то же самое, но относительно y (умножим уравнение на -1)
Получили то же самое, чего и следовало ожидать.
А вообще, это лишь частный случай и, по идее, тут и простым разложением на множители можно это сделать.
А вообще, это гораздо более общая задача, если уж обратиться к аналитической геометрии. Так как есть общее уравнение линии второго порядка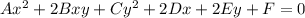
Есть теорема о приведении уравнения такого вида к одному из 9 канонических случаев. Это может быть: 1) эллипс, 2) гипербола, 3) парабола, 4) мнимый эллипс, 5) пара пересекающихся прямых, 6) пара мнимых пересекающихся прямых, 7) пара параллельных прямых, 8) пара мнимых параллельных прямых, 9) пара совпавших прямых.
Вот их уравнения по порядку. Причем это в новой системе координат, которая является результатом аффинных преобразований - поворота и переноса исходной системы координат. Если не углубляться в квадратичные формы, то нужно уметь считать определители и решать простенькие системы уравнений и немного знать тригонометрию. Координаты, угол и вид через большое количество действий вычисляются.
Если же идти через квадратичные формы, то там уже надо знать линейную алгебру (помимо определителей, обратных матриц, надо знать, как составлять матрицу квадратичной формы, знать про собственные вектора матрицы, уметь делать переходы к новому базису и т.д. и сделать можно в итоге через метод Лагранжа, а можно и через ортогональное преобразование).
То есть данная задача хороша на применение различных методов, которые были в свое время разработаны.
(P.S. цвета на графике разные, потому что просто хотел показать, где какая прямая, так как объединение множеств, то должно быть, по-хорошему, одного цвета)