Знайдіть найбільше значення функції f(x)=1\3-4x на [0;3]

Показать ответ

Ответ:

gangstarvegas3

25.12.2020 11:07

Набільше значення $\frac{4}{3}$

Объяснение:

$(f(x))'=(\frac{1}{3 - 4x})'=\frac{4}{(3 -4x)^{2} } \\(f(0))'=\frac{4}{(3 - 4*0)^{2} }=\frac{4}{3^{2} }=\frac{4}{9\\}\\(f(3))'=\frac{4}{(3 - 4 * 3)^{2} }=\frac{4}{81} \\(f(x))'=0\\\frac{4}{(3 -4x)^{2} }=0\\$

Коренів у рівняня 4 / (3 - 4x)(3 - 4x) немає так як знаменник не може дорівнювати нулю, отже функція на області визначення немає єкстремувів

$f(3)=\frac{4}{3-4x}=\frac{4}{3 - 4 * 3}=\frac{4}{3 - 12}=-\frac{4}{9}$ - найменше значення на проміжку

$f(0)=\frac{4}{3 -4x}=\frac{4}{3 - 4*0} =\frac{4}{3}$ - найбльше значення на проміжку

0,0(0 оценок)

Популярные вопросы: Алгебра

irazatula05

22.02.2023 12:17

Найдите скорость первого автомобиля...

Kylaguzzz

28.12.2021 02:40

Ть розв язати систему рівнянь 4х+2y=2, 5x-4y=9...

MarusiaG

01.06.2021 08:32

Ить систему рывнянь (x+y )*xy=6 (x-y)*xy=2...

alisha15sherban

15.09.2022 01:16

Разбейте функции на группы...

0Mishaj

11.03.2021 15:04

Найдите все значения переменной , при которых равны значения выражений 9х2 - х и 5х - 1...

oksana1410

12.01.2023 04:09

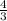
На тарелке 10 пирожков: 5 с мясом, 2 с капустой и 3 с вишней. андрей наугад выбирает один пирожок. найдите вероятность того, что он окажется с вишней. подробное объяснение...

АйданкаТоктогулова

12.01.2023 04:09

Решить по формулам 25a во второй степени -144...

stentani97

12.01.2023 04:09

Решите систему сложения 12х-7y=2 ; 4х-5у=6...

ИЛЬЯ2161

03.01.2022 06:41

Все выражение в корне 3х в квадрате - 12х кто нибудь, решите !...

ewenchester

03.01.2022 06:41

Решите уравнение, используя квадрат суммы и квадрат разности (7х-5)^2=7(x+1)^2...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку