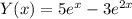Сначала разделим левую и правую часть уравнения на x, получим:
Решим сначала однородное уравнение, вида:
Это уравнение с разделяющимися переменными, получаем:
Берем интеграл от обоих частей получаем:
Дальше методом вариации свободной постоянной ищем частное решение неоднородного уравнения:
Представляем C как функцию от х, т.е C=C(x) и подставляем выражение в исходное уравнение. Получаем:
Сокращаем подобные и прочее, получаем:
Подставляем получившееся значение C(x) в выражение и получаем частное решение
В итоге общее решение неоднородного уравнения это сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Т.е.
Все, уравнение решено. Теперь решаем задачу Коши:
Т.к.
то приходим к уравнению
Все, нашли С, теперь пишем решение задачи Коши:
ответ: Общее решение дифференциального уравнения:
Частное решение дифференциального уравнения, удовлетворяющиего начальному условию :
Сначала решим общее однородное уравнение:
y''-4y'+3y=0
Для этого составим характеристическое уравнение:
Находим корни, получаем:
Тогда общее решение однородного уравнения запишется как:
Теперь найдем частное решение неоднородного уравнения.
Попробуем подобрать его, вообще тут видно, что частное решение этого уравнения будет
Если такой вариант нахождения частного решения не подходит, то можно решать все долго и по формулам:
для этого воспользуемся методом вариации постоянной, дл это представим C1 и С2 как функции от х и решим все по формуле:
Разделим первое и второе уравнениея на , выразим из 1го уравнения получим
Теперь подставим это во второе уравнение и получим, после всех сокращений:
Теперь найдем C1(x)
Подставляем найденные C1 и C2 и получаем:
Частное решение в виде:
Теперь найдем общее решение:
Y(x)=общее решение однородного уравнения+частное решение неоднородного уравнения
Я думаю что стоить взять частное решение которое было получено подбором, потому что оно проще, да и я мог где нибудь ошибиться в расчетах, поэтому:
(1)
Теперь решаем задачу Коши:
Она заключается в нахождении C1 и C2
Все просто, подставим в решение (1) вместо x число 0, а вместо y число 2 (это соответсвует y(0)=2)
Теперь возьмем производную и подставим в нее вместо x ноль, а вместо y -1
Получили систему уравнение:
Отсюда C2=0, C1=5.
Теперь запишем ответ:
ОТВЕТ:
Сначала разделим левую и правую часть уравнения на x, получим:
Решим сначала однородное уравнение, вида:
Это уравнение с разделяющимися переменными, получаем: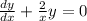
Берем интеграл от обоих частей получаем:
Дальше методом вариации свободной постоянной ищем частное решение неоднородного уравнения:
Представляем C как функцию от х, т.е C=C(x) и подставляем выражение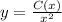 в исходное уравнение. Получаем:
в исходное уравнение. Получаем:
Сокращаем подобные и прочее, получаем:
Подставляем получившееся значение C(x) в выражение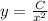 и получаем частное решение
и получаем частное решение 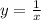
В итоге общее решение неоднородного уравнения это сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Т.е.
Все, уравнение решено. Теперь решаем задачу Коши:
Т.к.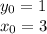
то приходим к уравнению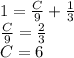
Все, нашли С, теперь пишем решение задачи Коши:
ответ: Общее решение дифференциального уравнения:
Частное решение дифференциального уравнения, удовлетворяющиего начальному условию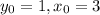 :
:
Сначала решим общее однородное уравнение:
y''-4y'+3y=0
Для этого составим характеристическое уравнение:
Находим корни, получаем:
Тогда общее решение однородного уравнения запишется как:
Теперь найдем частное решение неоднородного уравнения.
Попробуем подобрать его, вообще тут видно, что частное решение этого уравнения будет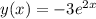
Если такой вариант нахождения частного решения не подходит, то можно решать все долго и по формулам:
для этого воспользуемся методом вариации постоянной, дл это представим C1 и С2 как функции от х и решим все по формуле:
Разделим первое и второе уравнениея на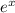 , выразим из 1го уравнения
, выразим из 1го уравнения 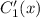 получим
получим 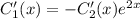
Теперь подставим это во второе уравнение и получим, после всех сокращений:
Подставляем найденные C1 и C2 и получаем:
Частное решение в виде:
Теперь найдем общее решение:
Y(x)=общее решение однородного уравнения+частное решение неоднородного уравнения
Я думаю что стоить взять частное решение которое было получено подбором, потому что оно проще, да и я мог где нибудь ошибиться в расчетах, поэтому:
Теперь решаем задачу Коши:
Она заключается в нахождении C1 и C2
Все просто, подставим в решение (1) вместо x число 0, а вместо y число 2 (это соответсвует y(0)=2)
Теперь возьмем производную и подставим в нее вместо x ноль, а вместо y -1
Получили систему уравнение:
Отсюда C2=0, C1=5.
Теперь запишем ответ:
ОТВЕТ: