Объяснение: Украинскую мову я не знаю, надеюсь, поймёте.
Пусть x - скорость велосипедиста на первом участке пути, т.е. с города Селятин до поселка городского типа Грибне. По условию известно, что расстояние между населёнными пунктами равно 20км. Тогда время, которое потратил велосипедист на дорогу в Грибне будет равно ч. На обратном пути из Грибне в Селятин велосипедист увеличил скорость на 1км/ч, т.е. его скорость на обратном пути - (x+1) км/ч. И на обратный путь он потратил на 5 минут меньше. До этого мы работали только с часами, а здесь нам даны минуты, поэтому необходимо перевести 5 минут в часы, т.к. это совершенно разные единицы измерения.
5мин=ч.
Время на обратном пути равно ч.
Помним, что расстояние между городами - 20км. Составим уравнение
(x+1)*()=20
(x+1)*()=20
-x²-x+240=0
x²+x-240=0
D=31²
x= - x - это скорость, поэтому она не может быть отрицательной, значение -16 - не подходит.
км/ч - скорость на первом участке пути с Селятин до Грибне.
х часов в пути будет находиться автомобиль, выехавший из города В до момента встречи с автомобилем, выехавшим из города А х(ч) + 30 мин = (х + 0,5) часов в пути будет находиться автомобиль, выехавший из города А до момента встречи с автомобилем, выехавшим из города В 80х (км автомобиль, выехавший из города А до момента встречи с автомобилем, выехавшим из города В 90(х + 0,5) = (90х + 45) (км автомобиль, выехавший из города В до момента встречи с автомобилем, выехавшим из города А Расстояние между городами А и В равно 555 км, с.у. 80х + 0,5 + 90х + 45 = 555 170х = 509,5 х ≈ 3 часа в пути будет находиться автомобиль, выехавший из города В до момента встречи с автомобилем, выехавшим из города А
ответ: 15км/ч.
Объяснение: Украинскую мову я не знаю, надеюсь, поймёте.
Пусть x - скорость велосипедиста на первом участке пути, т.е. с города Селятин до поселка городского типа Грибне. По условию известно, что расстояние между населёнными пунктами равно 20км. Тогда время, которое потратил велосипедист на дорогу в Грибне будет равно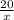 ч. На обратном пути из Грибне в Селятин велосипедист увеличил скорость на 1км/ч, т.е. его скорость на обратном пути - (x+1) км/ч. И на обратный путь он потратил на 5 минут меньше. До этого мы работали только с часами, а здесь нам даны минуты, поэтому необходимо перевести 5 минут в часы, т.к. это совершенно разные единицы измерения.
ч. На обратном пути из Грибне в Селятин велосипедист увеличил скорость на 1км/ч, т.е. его скорость на обратном пути - (x+1) км/ч. И на обратный путь он потратил на 5 минут меньше. До этого мы работали только с часами, а здесь нам даны минуты, поэтому необходимо перевести 5 минут в часы, т.к. это совершенно разные единицы измерения.
5мин=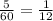 ч.
ч.
Время на обратном пути равно ч.
ч.
Помним, что расстояние между городами - 20км. Составим уравнение
(x+1)*( )=20
)=20
(x+1)*(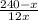 )=20
)=20
-x²-x+240=0
x²+x-240=0
D=31²
x=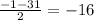 - x - это скорость, поэтому она не может быть отрицательной, значение -16 - не подходит.
- x - это скорость, поэтому она не может быть отрицательной, значение -16 - не подходит.
ответ: 15км/ч
Удачи!
х(ч) + 30 мин = (х + 0,5) часов в пути будет находиться автомобиль, выехавший из города А до момента встречи с автомобилем, выехавшим из города В
80х (км автомобиль, выехавший из города А до момента встречи с автомобилем, выехавшим из города В
90(х + 0,5) = (90х + 45) (км автомобиль, выехавший из города В до момента встречи с автомобилем, выехавшим из города А
Расстояние между городами А и В равно 555 км, с.у.
80х + 0,5 + 90х + 45 = 555
170х = 509,5
х ≈ 3 часа в пути будет находиться автомобиль, выехавший из города В до момента встречи с автомобилем, выехавшим из города А