Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
5
a
4
−
2
a
3
+
0
,
3
a
2
−
4
,
6
a
+
8
x
y
3
−
5
x
2
y
+
9
x
3
−
7
y
2
+
6
x
+
5
y
−
2
Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.
Например, многочлен
8
b
5
−
2
b
⋅
7
b
4
+
3
b
2
−
8
b
+
0
,
25
b
⋅
(
−
12
)
b
+
16
можно упростить.
Представим все слагаемые в виде одночленов стандартного вида:
Единица - число целое, его и не рассматриваем, главное, чтобы дробь принимала целые значения. Как этого добиться?
Можно по-разному сгруппировать множители, есть два варианта, рассмотрим каждый из них и в конце объединим полученные значения
1) рассмотрим случай, когда
В этом случае 4 делится на , такие значения легко подбираются, самое главное найти те
пусть делится на , тогда частное от деления некоторое число
Немного преобразуем, умножив на (оно не равно 0 ещё по условию)
Нужно решить полученное уравнение в целых числах. В данном случае все просто: произведение целых чисел равно единице либо когда каждое из чисел равно 1, либо -1.
То есть 1 вариант, когда
либо 2 вариант, когда
Самое главное, что 4 делится на оба полученных значения , то есть они точно пойдут в ответ.
Теперь рассматриваем случай 2):
считаем, что не делится на нацело (когда делится, мы уже такие случаи нашли), и тогда остается только вариант такой:
Понятно, что при целых правый сомножитель всегда будет целым, значит, нужно добиться, чтобы левый тоже был целым.
Если совсем просто, то заменим , и имеем тогда выражение
, которое должно быть целым, отсюда следует, что является делителем числа 4, а их немного на самом деле.
Правда, вспоминаем, что
Нам нужны целые числа, поэтому значения с корнями откидываются, а ещё вспоминаем, что общий ответ получается путем объединения случаев 1 и 2, но нам повезло, оба значения из случая 1 вошли в значения случая 2.
Вообще есть ещё случай группировки 3:
Но тут сразу видно, что при целых делимость нацело правого множителя невозможна при (парабола растет быстрее прямой), а
(которые, к слову, сюда тоже подходят) мы уже рассмотрели.
Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
5
a
4
−
2
a
3
+
0
,
3
a
2
−
4
,
6
a
+
8
x
y
3
−
5
x
2
y
+
9
x
3
−
7
y
2
+
6
x
+
5
y
−
2
Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.
Например, многочлен
8
b
5
−
2
b
⋅
7
b
4
+
3
b
2
−
8
b
+
0
,
25
b
⋅
(
−
12
)
b
+
16
можно упростить.
Представим все слагаемые в виде одночленов стандартного вида:
8
b
5
−
2
b
⋅
7
b
4
+
3
b
2
−
8
b
+
0
,
25
b
⋅
(
−
12
)
b
+
16
=
=
8
b
5
−
14
b
5
+
3
b
2
−
8
b
−
3
b
2
+
16
Приведем в полученном многочлене подобные члены:
8
b
5
−
14
b
5
+
3
b
2
−
8
b
−
3
b
2
+
16
=
−
6
b
5
−
8
b
+
16
Итак, есть выражение
Единица - число целое, его и не рассматриваем, главное, чтобы дробь принимала целые значения. Как этого добиться?
Можно по-разному сгруппировать множители, есть два варианта, рассмотрим каждый из них и в конце объединим полученные значения
1) рассмотрим случай, когда
В этом случае 4 делится на , такие значения легко подбираются, самое главное найти те
, такие значения легко подбираются, самое главное найти те
пусть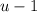 делится на
делится на  , тогда частное от деления некоторое число
, тогда частное от деления некоторое число 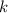
Немного преобразуем, умножив на (оно не равно 0 ещё по условию)
(оно не равно 0 ещё по условию)
Нужно решить полученное уравнение в целых числах. В данном случае все просто: произведение целых чисел равно единице либо когда каждое из чисел равно 1, либо -1.
То есть 1 вариант, когда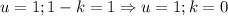
либо 2 вариант, когда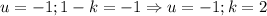
Самое главное, что 4 делится на оба полученных значения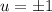 , то есть они точно пойдут в ответ.
, то есть они точно пойдут в ответ.
Теперь рассматриваем случай 2):
считаем, что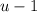 не делится на
не делится на  нацело (когда делится, мы уже такие случаи нашли), и тогда остается только вариант такой:
нацело (когда делится, мы уже такие случаи нашли), и тогда остается только вариант такой:
Понятно, что при целых правый сомножитель всегда будет целым, значит, нужно добиться, чтобы левый тоже был целым.
правый сомножитель всегда будет целым, значит, нужно добиться, чтобы левый тоже был целым.
Если совсем просто, то заменим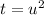 , и имеем тогда выражение
, и имеем тогда выражение
Правда, вспоминаем, что
Нам нужны целые числа, поэтому значения с корнями откидываются, а ещё вспоминаем, что общий ответ получается путем объединения случаев 1 и 2, но нам повезло, оба значения из случая 1 вошли в значения случая 2.
Вообще есть ещё случай группировки 3:
Но тут сразу видно, что при целых делимость нацело правого множителя невозможна при
делимость нацело правого множителя невозможна при 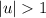 (парабола растет быстрее прямой), а
(парабола растет быстрее прямой), а
ответ: