Кроме этого, известно, что основной период котангенса равен :
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: .
Запишем:
Действительно, , арккотангенс может принимать такое значение.
Известно соотношение:
Кроме этого, известно, что основной период котангенса равен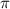 :
:
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида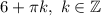 , чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
Выполним оценку обеих частей неравенства:
Получим:
Или записывая соотношение для k:
Единственное подходящее целое значение: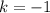 .
.
Запишем:
Действительно, , арккотангенс может принимать такое значение.
, арккотангенс может принимать такое значение.
ответ: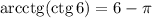
Объяснение:
+ - + - +
_____-3_________2/3______1___________3_______
x∈(-∞;3)∪[2/3; 1]∪(3; +∞)
+ - + - +
_______-6____________-2______1______2______
x∈(-∞; -6]∪(-2; 1]∪(2; +∞)
+ - + - +
_____-5__________-2_____0____0,5______
x∈(-∞; -5)∪(-2; 0)∪(0,5; +∞)
+ - + - +
_______0_______2______3_________7________
x∈(0;2)∪(3;7)