Число делится на 4, если число, составленное из последних двух цифр, делится на 4. В данном случае это 37628 (ведь 28 делится на 4).
ответ: 37628.
Второе задание
Преобразуем это число по правилам действий со степенями:
Число оканчивается на 6, потому что любое число, оканчивающееся на 6, в любой степени тоже оканчивается на 6. Затем, если мы умножим это число на 8, то получим число, оканчивающееся на 8 (потому что ).
ответ: на 8.
Третье задание
Преобразуем выражение по правилам действий со степенями:
ответ: на 7.
***
Если будут какие-нибудь вопросы — задавайте.
Если мой ответ оказался полезен, отмечайте его как «лучший ответ».
Первое задание
Число делится на 4, если число, составленное из последних двух цифр, делится на 4. В данном случае это 37628 (ведь 28 делится на 4).
ответ: 37628.
Второе задание
Преобразуем это число по правилам действий со степенями:
Число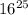
оканчивается на 6, потому что любое число, оканчивающееся на 6, в любой степени тоже оканчивается на 6. Затем, если мы умножим это число на 8, то получим число, оканчивающееся на 8 (потому что 
).
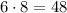ответ: на 8.
Третье задание
Преобразуем выражение по правилам действий со степенями:
ответ: на 7.
***
Если будут какие-нибудь вопросы — задавайте.
Если мой ответ оказался полезен, отмечайте его как «лучший ответ».
x²-(√6-√24)x-12=0
1) Упростим выражение (√6-√24).
√6-√24 = √6-√(4·6) = √6-2√6 = - √6
2) Подставим в данное уравнение и получим:
x² - (-√6)x - 12 = 0
x² + √6x - 12 = 0
3) Решаем уравнение
x² + √6x - 12 = 0
D = 6 - 4·1·(-12) = 6 + 48 = 54
√D = √54 = √(9·6) = 3√6
x₁ = (- √6 - 3√6)/2 = - 4√6/2 = - 2√6
x₂ = (- √6 + 3√6)/2 = 2√6/2 = √6
4) Находим целые числа, заключенные между корнями уравнения
x₁ = - 2√6 ≈ - 4,9
x₂ = √6 ≈ 2,45
{- 4; - 3; - 2; - 1; 0; 1; 2}
И, наконец, находим их сумму:
- 4 - 3 - 2 - 1 + 0 + 1 + 2 = - 7
ответ: - 7.