Аня, Боря и Вася делят 12 различных открыток (возможно совсем несправедливо). Сколько имеется это сделать так, чтобы самая красивая открытка досталась не Васе?
Каждому из вариантов распределения открыток можем сопоставить число записанное в троичной системе счисления (например 0 соответствует Ане, 1 - Боре, 2 - Васе). Всего 12 значных чисел в троичной системе счисления будет
Чтобы самая красивая открытка не досталась Васе (т.е. чтобы в одной позиций 12-значного числа не было цифры 2) вариантов будет
Аня, Боря и Вася делят 12 различных открыток (возможно совсем несправедливо). Сколько имеется это сделать так, чтобы самая красивая открытка досталась не Васе?
Каждому из вариантов распределения открыток можем сопоставить число записанное в троичной системе счисления (например 0 соответствует Ане, 1 - Боре, 2 - Васе). Всего 12 значных чисел в троичной системе счисления будет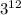
Чтобы самая красивая открытка не досталась Васе (т.е. чтобы в одной позиций 12-значного числа не было цифры 2) вариантов будет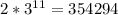
x ^3 - 3x^2 + 3x - 1 - (x^3 -3x^2 + 3x - 1) = 6x^2 + 2x
6x^2 + 2x = 0
2x (3x + 1) = 0
2x = 0
x1 = 0
3x + 1 = 0
3x = - 1
x2 = - 1/3
№3
x^3 + 3x^2*2 + 3x*4 + 8 - ( x^3 - 3x^2 + 3x -1) = 9x^2 + 36
x*3 + 6x^2 + 12x + 8 - x^3 + 3x^2 - 3x + 1) = 9x^2 + 36
x^3 + 6x^2 - 9x^2 + 12x + 8 - 36 -x^3 + 3x^2 - 3x + 1 = 0
12x - 3x -28 + 1 = 0
9x = 28 - 1
9x = 27
x = 3
№4
x^3 + 9x^2 + 27x + 27 - x^3 - 9x^2 = 0
27x = - 27
x = - 1
№2
х^3 - 6x^2 +12x - 8 -3x^2 -4 = x^3 - 9x^2 + 27x - 27
x^3 - 6x^2 + 12x - 8 - 3x^2 -4 - x^3 + 9x^2 - 27x + 27 = 0
12x - 12 - 27x + 27 = 0
- 15x = -27 + 12
- 15x = - 15
x = 1