А теперь подумаем, что будет при взятии целой части числа.
Вот, допустим, f(x)=1 без взятия целой части, при , тогда при любом , но при взятии целой части будет 1. Далее, при некотором , f(x)=2.
Но при любом
При идет прямая, в точка не выколота, а вот в где f(x)=1 выколота, а вот где f(x)=2 не выколота.
И так далее.
При f(x)<0 все симметрично наоборот
На рисунке я постарался отметить все, что нужно. Синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
Пунктирами, по факту, отмечены разрывы функции. Это перпендикуляры к кусочкам графика
log7 log1/3 log8 x < 0
log7 log1/3 log8 x < log7 1
log1/3 log8 x < 1
log1/3 log8 x < log1/3 1/3
log8 x > 1/3 основание меньше 1 (1/3) - знак поменяли
log8 x > log8 8^1/3
x > 2
упс забыли про ОДЗ - логарифм log(a) b определен, когда a>0, b>0, a≠1
значит пишем все ограничения и решаем систему
x>0
log1/3 log8 x > 0, log1/3 log8 x > log1/3 1 (основание меньше 1, меняем знак) log8 x < 1. log8 x < log8 8, x<8
log8 x > 0 , log8 x > log8 1 , x>1
Итак ОДЗ x ∈ (1 8)
смотрим решение и ОДЗ и пишем ответ
ответ x ∈ (2, 8)
Сначала построим график f(x)=2x+3.4
А теперь подумаем, что будет при взятии целой части числа.
Вот, допустим, f(x)=1 без взятия целой части, при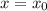
, тогда при любом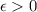 
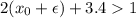, но при взятии целой части будет 1. Далее, при некотором 
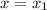, f(x)=2.
Но при любом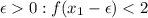
При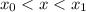
идет прямая, в 
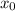точка не выколота, а вот в 
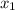где f(x)=1 выколота, а вот где f(x)=2 не выколота.
И так далее.
При f(x)<0 все симметрично наоборот
На рисунке я постарался отметить все, что нужно. Синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
Пунктирами, по факту, отмечены разрывы функции. Это перпендикуляры к кусочкам графика