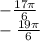Я заметил, что в каждом примере из указанных выше все полиномы "взаимоуничтожают" друг друга (а именно одни и те же слагаемые со знаком "+" и со знаком "-"), поэтому в каждом примере всё сводится к равенству левой и правой частей, из этого делаем вывод, что решением будет любое действительное число, ибо каким бы числом не была переменная, равенство всё равно будет выполняться.
a) x ∈ R
b) m ∈ R
c) x ∈ R
d) x ∈ R
e) a ∈ R
f) m ∈ R
g) x ∈ R
h) y ∈ R
i) a ∈ R
j) m ∈ R
Объяснение:
Я заметил, что в каждом примере из указанных выше все полиномы "взаимоуничтожают" друг друга (а именно одни и те же слагаемые со знаком "+" и со знаком "-"), поэтому в каждом примере всё сводится к равенству левой и правой частей, из этого делаем вывод, что решением будет любое действительное число, ибо каким бы числом не была переменная, равенство всё равно будет выполняться.
a) (x² + x) + (x² - 4x) + (4 - 2x² + 4x) = x + 4,
x² + x + x² - 4x + 4 - 2x² + 4x = x + 4,
x + 4 = x + 4,
x ∈ R (любое действительное число)
b) m² - 64 - m² - 4m + 64 = -4m,
-4m = -4m,
m ∈ R (любое действительное число)
c) (x³ - 1) + (x³ - x²) - (2x³ - x²) = -1,
x³ - 1 + x³ - x² - 2x³ + x² = -1,
-1 = -1,
x ∈ R (любое действительное число)
d) (2x² - 10x + 25) - (2x² + 5x - 10) = -15x + 35,
2x² - 10x + 25 - 2x² - 5x + 10 = -15x + 35,
-15x + 35 = -15x + 35,
x ∈ R (любое действительное число)
e) (a² + 1) + (2a² + a) - (3a² - a) = 2a + 1,
a² + 1 + 2a² + a - 3a² + a = 2a + 1,
2a + 1 = 2a + 1,
a ∈ R (любое действительное число)
f) (m² + m - 1) + (2m² - m + 3) = (6m² + 4) - (3m² + 2),
m² + m - 1 + 2m² - m + 3 = 6m² + 4 - 3m² - 2,
3m² + 2 = 3m² + 2,
m ∈ R (любое действительное число)
g) (2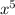 - 3
- 3 + 5) - (
+ 5) - (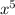 - 3
- 3 + 6) = (7
+ 6) = (7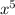 + 8) - (6
+ 8) - (6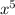 + 9),
+ 9),
2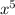 - 3
- 3 + 5 -
+ 5 - 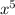 + 3
+ 3 - 6 = 7
- 6 = 7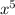 + 8 - 6
+ 8 - 6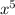 - 9,
- 9,
x ∈ R (любое действительное число)
h) (6 - 8
- 8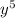 - y) - (6
- y) - (6 + 2
+ 2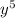 - 2y) = (9
- 2y) = (9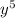 +
+ 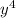 - y) - (19
- y) - (19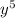 +
+ 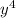 - 2y),
- 2y),
6 - 8
- 8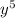 - y - 6
- y - 6 - 2
- 2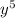 + 2y = 9
+ 2y = 9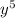 +
+ 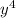 - y - 19
- y - 19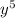 -
- 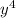 + 2y,
+ 2y,
-10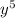 + y = -10
+ y = -10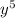 + y,
+ y,
y ∈ R (любое действительное число)
i) (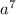 - 2
- 2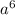 - 3
- 3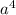 ) - (-
) - (-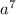 - 2
- 2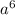 + 5
+ 5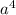 ) = (3
) = (3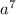 - 5
- 5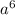 ) - (
) - (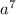 - 5
- 5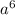 + 8
+ 8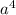 ),
),
2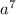 - 8
- 8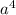 = 2
= 2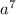 - 8
- 8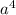 ,
,
a ∈ R (любое действительное число)
j) (5m³ - 4m²) + (-m³ + 2m² - 3) = (6m³ - 2m² - 5) + (-2m³ + 2),
5m³ - 4m² -m³ + 2m² - 3 = 6m³ - 2m² - 5 - 2m³ + 2,
4m³ - 2m² - 3 = 4m³ - 2m² - 3,
m ∈ R (любое действительное число)
Так как функция косинус по модулю не превосходит единицы в поле действительных чисел, то выбираем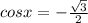
Далее решаем это уравнение:
По условию нужно найти корни на промежутке![[-\frac{7\pi}{2}; -2\pi]](/tpl/images/1359/8515/36df4.png) .
.
Это можно сделать несколькими например, с неравенства:
Рассмотрим случай, когда 5 имеет знак "плюс":
Очевидно, что из целых k подходит k = -2.
Теперь рассмотрим случай, когда 5 имеет знак "минус":
k = -1 нам подходит.
Теперь подставляем полученные k в серию корней:
1) Когда плюс - k = -2, т. е.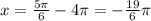
2) Когда минус - k = -1, т. е.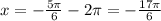
ответ: а)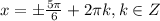
б)