Из второго уравнения системы выразим через , получим:
--------(1)
Поскольку не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо выражение (1), мы не потеряем решений системы:
, отсюда
, отсюда
---------(2)
Замена: пусть , тогда (2) примет вид:
--------(3)
(3) - квадратное уравнение относительно
Но второй корень не удовлетворяет условию
Возвращаясь к старой неизвестной, получим:
-------(4)
Из (4) получаем два значения :
Подставим в первое уравнение системы вместо выражение (4), найдем соответствующие значения :
Дана система уравнений:
Из второго уравнения системы выразим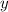 через
через  , получим:
, получим:
Поскольку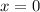 не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо
не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо 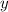 выражение (1), мы не потеряем решений системы:
выражение (1), мы не потеряем решений системы:
Замена: пусть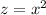 , тогда (2) примет вид:
, тогда (2) примет вид:
(3) - квадратное уравнение относительно
Но второй корень не удовлетворяет условию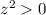
Возвращаясь к старой неизвестной, получим:
Из (4) получаем два значения :
:
Подставим в первое уравнение системы вместо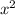 выражение (4), найдем соответствующие значения
выражение (4), найдем соответствующие значения 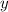 :
:
Из (5) получаем два значения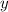 :
:
Итак, наша система имеет четыре решения:
1)корень 2 sin 2x=1
sin2x= (корень из 2)/2
2x=(-1)^n*arcsin(корень 2/2)+пn, n принадлежит целым числам
x=(-1)^n*п/8+п/2*n, n принадлежит целым числам
ответ: (-1)^n*п/8+п/2*n, n принадлежит целым числам
2) sin(4x+п/8)=0
4x+п/8= пn, n принадлежит целым числам
4x=-п/8+пn, n принадлежит целым числам
x=-п/32+п/4*n, n принадлежит целым числам
ответ: -п/32+п/4*n, n принадлежит целым числам
3) sin (x/2 + п/3)-1=0
sin (x/2 + п/3)=1
x/2+п/3=п/2+2пn, n принадлежит целым числам
x/2=п/2 -п/3 + 2пn, n принадлежит целым числам
x=п- 2п/3 + 4пn, n принадлежит целым числам
х=п/3+4пn, n принадлежит целым числам
ответ: п/3+4пn, n принадлежит целым числам
4)sin(x-п/8)=-1
x-п/8=-п/2+2пn, n принадлежит целым числам
x= п/8-п/2+2пn, n принадлежит целым числам
x=-3п/2+2пn, n принадлежит целым числам
ответ: -3п/2+2пn, n принадлежит целым числам
5) cosx=-2, т.к. облсать значений функции cosx [-1;1], то данное уравнение не имеет решений.