ответ: 25
Объяснение:
Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х==20
Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.
Используя отношение найдем второй катет большого треугольника через маленькие:
, где х=15
Найдем гипотенузу через формулы площади треугольника.
S=, где а=16+х, h=12
а=16+х-гипотенуза
S=, где sin90=1, а=20, b=15.
S==150
150=, а==25.
получится дробь, у которой числитель = 2( х + 1) -(х² - х + 1) - 2х + 1=
=2х + 2 - х² + х - 1 - 2х + 1 = - х² + х + 2
В знаменателе : х³ +1
Неравенство запишем (- х² + х + 2)/( х³ + 1) ≥ 0
(х² - х - 2)/(х³ +1) ≤ 0
(х - 2)( х + 1)/(х³ + 1) ≤ 0
(х - 2)/(х² - х + 1) ≤ 0
х² - х + 1 всегда > 0,⇒х - 2 ≤ 0⇒ х ≤ 2 ( х ≠ -1)
ответ х∈ ( -∞ ; -1)∨(-1; 2]
наибольшее целое х = 2
2)Числитель (х - 3)(х + 10)(х + 9)(х - 1)
Знаменатель (х +9)( х - 1)
После сокращения получим неравенство: (х - 3)(х + 10)<0
-∞ + -10 - -9 - 1 - 3 + +∞
ответ х ∈(-10; -9)∨(-9; 1)∨(1; 3)
ответ: 25
Объяснение:
Рассмотрим треугольник со сторонами 16 и 12, в нем неизвестная сторона будет равна: х=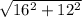 =20
=20
Воспользуемся свойством высоты в прямоугольном треугольнике, проведенной из прямого угла:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных ему, каждый из которых подобен данному.
Используя отношение найдем второй катет большого треугольника через маленькие:
Найдем гипотенузу через формулы площади треугольника.
S=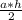 , где а=16+х, h=12
, где а=16+х, h=12
а=16+х-гипотенуза
S=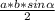 , где sin90=1, а=20, b=15.
, где sin90=1, а=20, b=15.
S=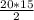 =150
=150
150=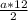 , а=
, а=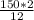 =25.
=25.