2) число -20 - отрицательное, оно больше числа 5,7. Так что будем отнимать от -20 5,7. -20 - 5,7 = - 14,3. ответ в этом примере получится отрицательный, так как -20 больше
4) Для того, чтобы поделить десятичные дроби, нужно перенести все запятые вправо так, чтобы мы делили на целое число. В данном случае, мы будем делить 187,5 на 75. 187 делить на 75 = 2 (целая часть). После целой части мы ставим запятую и делим 375 (остаток от деления) на 75. И получаем 5. ответ: 2,5
6) Складываем целые части дробей с целыми, а десятичные с десятичными. 54 + 5, А 7 + 63. Не забываем добавлять остатки от десятичных частей к целым. Получаем 60,33
8)Самое обыкновенное умножение. Можно решать столбиком. Каждое число друг под другом. Умножаем все числа друг на друга. Получаем 21,14
10) Переводим смешанную дробь 1 в неправильную. (1 * 14) + 5 = . Домножаем первую дробь на 2, чтобы получить общий знаменатель 14. Теперь решаем = . Умножаем на 12,6. Для удобства переведем 12,6 в неправильную дробь . Числитель умножаем на числитель, а знаменатель на знаменатель. Получим . Делим числитель на знаменатель и получаем 22,5
12) Переводим смешанные дроби в скобках в неправильные. Получим и . Приводим их к общему знаменателю, равному 90. Для этого домножаем первую дробь на 10, а вторую на 9. Получим и . Отнимаем дроби друг от друга. Для этого отнимаем числитель 320 - 198. Получаем 122. : . Чтобы поделить первую дробь на вторую, вторую дробь нужно перевернуть. Получим * 90. Сокращаем 90, получаем 122.
14) Чтобы не пришлось возводить оба больших числа в квадрат, вынесем степень за скобку . Получаем . 152 умножаем на 152, получаем 23104. 23104 делим на 100, то есть переносим запятую на 2 числа (число нолей в 100) влево. Получаем 231,04
16) Переведем смешанную дробь 6 в неправильную = . Делим дроби друг на друга. Для этого перевернем вторую дробь. * .
Сокращаем 13. 82 делим на 2. Получаем 41.
18) Сократим 24,2 и 0,242. Поделим числа друг на друга. Получим 100.
Сократим 35,6 и 3,56. Получим 10. 10 * 100 = 1000
20) Умножим на каждое число в скобках. Получим . . Вынесем числа из под корня. Получаем 10 + 5 = 15
22) Возводим в квадрат. = 16 = 7. 16 * 7 = 112. 112 делим на 16, получаем 7
Физический процесс протекает во времени, поэтому все физические формулы, описывающие явления материального мира во времени являются функциями, описывающими реальные физические процессы. В такие уравнения время входит в качестве переменного параметра, а не константы (как, например, в формуле для периода), либо входит опосредованно в другие величины, такие, например, как скорость, электрический ток и т.п. Некоторые уравнения описывают процессы и одновременно состояния, а поэтому не содержат непосредственно в себе параметра времени, а лишь показывают некоторые частные состояния системы, как, например уравнение Менделеева-Клайперона (уравнение идеального газа).
Уравнение равномерного движения – это функция, описывающая реальный физический процесс равномерного движения:
;
Уравнение равномерного прямолинейного движения – это функция, описывающая реальный физический процесс прямолинейного движения в векторном виде:
;
Следствие для скорости из уравнения определения ускорения – это функция, описывающая реальный физический процесс равномерного изменения скорости:
либо в векторном виде: ;
Уравнение равнопеременного движения – это функция, описывающая реальный физический процесс равнопеременного движения:
либо в векторном виде: ;
Второй Закон Ньютона – это функция, описывающая реальный физический процесс динамики движения:
либо в векторном виде: ;
Уравнение равномерного движения по окружности – это функция, описывающая реальный физический процесс равномерного движения по окружности:
;
Уравнение движения при гармонических колебаниях – это функция, описывающая реальный физический процесс гармонического колебания:
;
Следствие для скорости из уравнения гармонических колебаний – это функция, описывающая реальный физический процесс изменения скорости в гармоническом колебании:
;
Следствие для ускорения из уравнения гармонических колебаний – это функция, описывающая реальный физический процесс изменения ускорения в гармоническом колебании:
;
Следствие для энергии из уравнения определения теплоёмкости – это функция, описывающая реальный физический процесс нагревания:
где либо в удельном виде: ;
Следствие для энергии из уравнения определения теплоты плавления и кристаллизации – это функция, описывающая реальный физический процесс плавления и кристаллизации:
;
Следствие для энергии из уравнения определения теплоты парообразования и конденсации – это функция, описывающая реальный физический процесс парообразования и конденсации:
;
Следствие для энергии из уравнения определения теплоты горения – это функция, описывающая реальный физический процесс горения:
;
Уравнение идеального газа – это многопараметрическая функция, описывающая все физические процессы газов низких давлений:
;
Уравнения определения тока – это функция, описывающая реальный физический процесс движени заряженных частиц:
;
Закон Фарадея – это многопараметрическая функция, описывающая гальванический процесс:
где ;
Закон Ома – это функция, описывающая реальный физический процесс движения заряженных частиц в однородном проводнике:
;
Закон Джоуля-Ленца – это функция, описывающая реальный физический процесс превращения энергии в электрических цепях:
либо в мощностном виде: ;
Закон Ампера (Второй Закон Максвелла) – это функция, описывающая реальный физический процесс воздействия магнитного поля на проводник с током:
;
Закон Лоренца (Второй Закон Максвелла) – это функция, описывающая реальный физический процесс воздействия магнитного поля на движущуюся частицу:
;
Закон Фарадея-Ленца электромагнитной Индукции (Третий Закон Максвелла) – это функция, описывающая реальный физический процесс порождения вихревого электрического поля при изменении магнитного поля:
2) - 14,3
4) 2,5
6) 60,33
8) 21,14
10) 22,5
12) 122
14) 231,04
16) 41
18) 1000
20) 15
22) 7
Объяснение:
2) число -20 - отрицательное, оно больше числа 5,7. Так что будем отнимать от -20 5,7. -20 - 5,7 = - 14,3. ответ в этом примере получится отрицательный, так как -20 больше
4) Для того, чтобы поделить десятичные дроби, нужно перенести все запятые вправо так, чтобы мы делили на целое число. В данном случае, мы будем делить 187,5 на 75. 187 делить на 75 = 2 (целая часть). После целой части мы ставим запятую и делим 375 (остаток от деления) на 75. И получаем 5. ответ: 2,5
6) Складываем целые части дробей с целыми, а десятичные с десятичными. 54 + 5, А 7 + 63. Не забываем добавлять остатки от десятичных частей к целым. Получаем 60,33
8)Самое обыкновенное умножение. Можно решать столбиком. Каждое число друг под другом. Умножаем все числа друг на друга. Получаем 21,14
10) Переводим смешанную дробь 1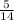 в неправильную. (1 * 14) + 5 =
в неправильную. (1 * 14) + 5 = 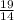 . Домножаем первую дробь на 2, чтобы получить общий знаменатель 14. Теперь решаем
. Домножаем первую дробь на 2, чтобы получить общий знаменатель 14. Теперь решаем  =
= 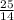 . Умножаем на 12,6. Для удобства переведем 12,6 в неправильную дробь
. Умножаем на 12,6. Для удобства переведем 12,6 в неправильную дробь 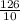 . Числитель умножаем на числитель, а знаменатель на знаменатель. Получим
. Числитель умножаем на числитель, а знаменатель на знаменатель. Получим 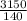 . Делим числитель на знаменатель и получаем 22,5
. Делим числитель на знаменатель и получаем 22,5
12) Переводим смешанные дроби в скобках в неправильные. Получим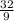 и
и 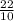 . Приводим их к общему знаменателю, равному 90. Для этого домножаем первую дробь на 10, а вторую на 9. Получим
. Приводим их к общему знаменателю, равному 90. Для этого домножаем первую дробь на 10, а вторую на 9. Получим 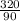 и
и 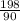 . Отнимаем дроби друг от друга. Для этого отнимаем числитель 320 - 198. Получаем 122.
. Отнимаем дроби друг от друга. Для этого отнимаем числитель 320 - 198. Получаем 122. 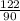 :
: 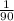 . Чтобы поделить первую дробь на вторую, вторую дробь нужно перевернуть. Получим
. Чтобы поделить первую дробь на вторую, вторую дробь нужно перевернуть. Получим 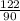 * 90. Сокращаем 90, получаем 122.
* 90. Сокращаем 90, получаем 122.
14) Чтобы не пришлось возводить оба больших числа в квадрат, вынесем степень за скобку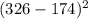 . Получаем
. Получаем 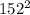 . 152 умножаем на 152, получаем 23104. 23104 делим на 100, то есть переносим запятую на 2 числа (число нолей в 100) влево. Получаем 231,04
. 152 умножаем на 152, получаем 23104. 23104 делим на 100, то есть переносим запятую на 2 числа (число нолей в 100) влево. Получаем 231,04
16) Переведем смешанную дробь 6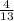 в неправильную =
в неправильную = 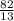 . Делим дроби друг на друга. Для этого перевернем вторую дробь.
. Делим дроби друг на друга. Для этого перевернем вторую дробь. 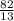 *
* 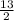 .
.
Сокращаем 13. 82 делим на 2. Получаем 41.
18) Сократим 24,2 и 0,242. Поделим числа друг на друга. Получим 100.
Сократим 35,6 и 3,56. Получим 10. 10 * 100 = 1000
20) Умножим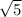 на каждое число в скобках. Получим
на каждое число в скобках. Получим 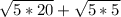 .
. 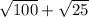 . Вынесем числа из под корня. Получаем 10 + 5 = 15
. Вынесем числа из под корня. Получаем 10 + 5 = 15
22) Возводим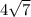 в квадрат.
в квадрат. 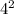 = 16
= 16 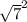 = 7. 16 * 7 = 112. 112 делим на 16, получаем 7
= 7. 16 * 7 = 112. 112 делим на 16, получаем 7
Уравнение равномерного движения – это функция, описывающая реальный физический процесс равномерного движения:
Уравнение равномерного прямолинейного движения – это функция, описывающая реальный физический процесс прямолинейного движения в векторном виде:
Следствие для скорости из уравнения определения ускорения – это функция, описывающая реальный физический процесс равномерного изменения скорости:
Уравнение равнопеременного движения – это функция, описывающая реальный физический процесс равнопеременного движения:
Второй Закон Ньютона – это функция, описывающая реальный физический процесс динамики движения:
Уравнение равномерного движения по окружности – это функция, описывающая реальный физический процесс равномерного движения по окружности:
Уравнение движения при гармонических колебаниях – это функция, описывающая реальный физический процесс гармонического колебания:
Следствие для скорости из уравнения гармонических колебаний – это функция, описывающая реальный физический процесс изменения скорости в гармоническом колебании:
Следствие для ускорения из уравнения гармонических колебаний – это функция, описывающая реальный физический процесс изменения ускорения в гармоническом колебании:
Следствие для энергии из уравнения определения теплоёмкости – это функция, описывающая реальный физический процесс нагревания:
Следствие для энергии из уравнения определения теплоты плавления и кристаллизации – это функция, описывающая реальный физический процесс плавления и кристаллизации:
Следствие для энергии из уравнения определения теплоты парообразования и конденсации – это функция, описывающая реальный физический процесс парообразования и конденсации:
Следствие для энергии из уравнения определения теплоты горения – это функция, описывающая реальный физический процесс горения:
Уравнение идеального газа – это многопараметрическая функция, описывающая все физические процессы газов низких давлений:
Уравнения определения тока – это функция, описывающая реальный физический процесс движени заряженных частиц:
Закон Фарадея – это многопараметрическая функция, описывающая гальванический процесс:
Закон Ома – это функция, описывающая реальный физический процесс движения заряженных частиц в однородном проводнике:
Закон Джоуля-Ленца – это функция, описывающая реальный физический процесс превращения энергии в электрических цепях:
либо в мощностном виде:
Закон Ампера (Второй Закон Максвелла) – это функция, описывающая реальный физический процесс воздействия магнитного поля на проводник с током:
Закон Лоренца (Второй Закон Максвелла) – это функция, описывающая реальный физический процесс воздействия магнитного поля на движущуюся частицу:
Закон Фарадея-Ленца электромагнитной Индукции (Третий Закон Максвелла) – это функция, описывающая реальный физический процесс порождения вихревого электрического поля при изменении магнитного поля: