Завдання 1:
Координати точки, яка належить графіку функції (або через яку проходить графік), будуть задовільняти формулу, якою ця функція задана.
Підставимо координати точки В (-2; у) у формулу: абсцису замість х, ординату замість у.
у = -3 ∙ (-2).
Тепер можемо обчислити ординату:
у = 6.
Відповідь: 6.
Завдання 2:
Підставимо координати точки N (-4; 9) у формулу: : абсцису замість х, ординату замість у.
a = 3.
Відповідь: 3.
Завдання 3:
Щоб вирішити рівняння графічно, треба побудувати графіки двох функцій:
та .
Коренями рівняння будуть абсциси точок перетину цих графіків.
Побудуємо графіки, створивши таблицю точок, що належать їм (див. малюнок).
Точка перетину графіків А (1;4).
х = 1.
Відповідь: 1.
Объяснение:
Первая система линейных уравнений:
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -4 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
2-ое уравнение умножаем на -1 и складываем с 3-им уравнением.
2-ое уравнение умножаем на -3 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
Получилась система, из которой можно получить фундаментальное решение:
x4, x5, x6 ∈ R
Вторая система решается точно также.
1-ое уравнение умножаем на -2 и складываем с 4-ым уравнением.
4-ое уравнение ставим 2-ым, от этого система не меняется:
2-ое уравнение умножаем на 5 и складываем с 3-им уравнением.
2-ое уравнение умножаем на 4 и складываем с 4-ым уравнением.
x4, x5 ∈ R
Завдання 1:
Координати точки, яка належить графіку функції (або через яку проходить графік), будуть задовільняти формулу, якою ця функція задана.
Підставимо координати точки В (-2; у) у формулу: абсцису замість х, ординату замість у.
у = -3 ∙ (-2).
Тепер можемо обчислити ординату:
у = 6.
Відповідь: 6.
Завдання 2:
Підставимо координати точки N (-4; 9) у формулу: : абсцису замість х, ординату замість у.
a = 3.
Відповідь: 3.
Завдання 3:
Щоб вирішити рівняння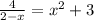 графічно, треба побудувати графіки двох функцій:
графічно, треба побудувати графіки двох функцій:
Коренями рівняння будуть абсциси точок перетину цих графіків.
Побудуємо графіки, створивши таблицю точок, що належать їм (див. малюнок).
Точка перетину графіків А (1;4).
х = 1.
Відповідь: 1.
Объяснение:
Первая система линейных уравнений:
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -4 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
2-ое уравнение умножаем на -1 и складываем с 3-им уравнением.
2-ое уравнение умножаем на -3 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
Получилась система, из которой можно получить фундаментальное решение:
x4, x5, x6 ∈ R
Вторая система решается точно также.
1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.
1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.
1-ое уравнение умножаем на -2 и складываем с 4-ым уравнением.
Получаем нули при x1 во всех уравнениях, кроме 1-го:
4-ое уравнение ставим 2-ым, от этого система не меняется:
2-ое уравнение умножаем на 5 и складываем с 3-им уравнением.
2-ое уравнение умножаем на 4 и складываем с 4-ым уравнением.
Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:
3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:
Получилась система, из которой можно получить фундаментальное решение:
x4, x5 ∈ R