Число делится на 10 только в том случае, если оно оканчивается цифрой 0.
Посмотрим, какой цифрой оканчивается каждое слагаемое.
1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.
Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.
Т.к. оканчивается цифрой 1, то также оканчивается цифрой 1. Тогда число оканчивается цифрой 7.
2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:
Поскольку оканчивается цифрой 6, то также оканчивается цифрой 6.
3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:
Т.к. оканчивается цифрой 7, то также оканчивается цифрой 7.
В итоге слагаемые оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число оканчивается цифрой 0 - следовательно, оно таки делится на 10.
Число делится на 10 только в том случае, если оно оканчивается цифрой 0.
Посмотрим, какой цифрой оканчивается каждое слагаемое.
1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.
Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.
Т.к.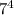
оканчивается цифрой 1, то 
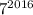также оканчивается цифрой 1. Тогда число 
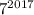оканчивается цифрой 7.
2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:
Поскольку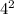
оканчивается цифрой 6, то 
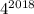также оканчивается цифрой 6.
3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:
Т.к.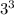
оканчивается цифрой 7, то 
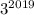также оканчивается цифрой 7.
В итоге слагаемые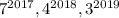
оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 
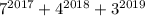оканчивается цифрой 0 - следовательно, оно таки делится на 10.
ОТВЕТ: да.
х³-3х²+(а+2)х-2а=0
х³-3х²+ах+2х-2а=0
х(х²-3х+2)+а(х-2)=0
х((х-2)(х-1))+а(х-2)=0
(х-2)(х(х-1)+а)=0
(х-2)(х²-х+а)=0
1) х-2=0 => х=2
Если уравнение должно иметь 2 противоположных корня, то второй множитель должен иметь один из корней, равный -2:
х²-х+а=0
(х+2)(х-3)=0
х²-х+6=0
Уравнение имеет 3 корня: х=2; х=-2; х=3.
Подставим все значения Х в уравнение:
1) х³-3х²+(а+2)х-2а=0
2³-3×2²+(а+2)×2-2а=0
8-12+2а+4-2а=0
0=0
2) х³-3х²+(а+2)х-2а=0
(-2)³-3×(-2)²+(а+2)×(-2)-2а=0
-8-12-2а-4-2а=0
-4а-24=0
а=-6
3) х³-3х²+(а+2)х-2а=0
3³-3×3²+(а+2)×3-2а=0
27-27+3а+6-2а=0
а=-6
ответ: а=-6