тяж. --- 3 арб. тяж 35 % от всех мал. 3 арб. мал. ?, но 5/13 остатка всего --- ? арб. Решение: 100 - 35 = 65 (%) остаток после больших 65 * (5/13) = 25 (%) --- составляет масса маленьких арбузов от всех 100 - 35 - 25 = 40 (%) составляет масса средних (проданных) арбузов от всех (35/3) % масса одного большого от всех арбузов (25/3) % масса одного маленького от всех Х арб. количество средних арбузов (40/Х) % масса одного среднего от массы всех арбузов 25/3 < 40/Х < 35/3 т.к. это средние по массе арбузы (каждый меньше тяжелого и большее маленького) 120/25 > Х > 120/35 4 ц 4/5 > X > 3 ц 3/7 Так как число арбузов целое, то единственное значение Х=4 , т.е. фермер продал 4 средних арбуза. 3 + 3 + 4 = 10 (арб). всего арбузов. ответ: 10 арбузов вырастил фермер.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила часов и против течения реки, на расстояние в 14 км, лодки затратила часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это часов. Составим уравнение:
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
тяж 35 % от всех
мал. 3 арб.
мал. ?, но 5/13 остатка
всего --- ? арб.
Решение:
100 - 35 = 65 (%) остаток после больших
65 * (5/13) = 25 (%) --- составляет масса маленьких арбузов от всех
100 - 35 - 25 = 40 (%) составляет масса средних (проданных) арбузов от всех
(35/3) % масса одного большого от всех арбузов
(25/3) % масса одного маленького от всех
Х арб. количество средних арбузов
(40/Х) % масса одного среднего от массы всех арбузов
25/3 < 40/Х < 35/3 т.к. это средние по массе арбузы (каждый меньше тяжелого и большее маленького)
120/25 > Х > 120/35
4 ц 4/5 > X > 3 ц 3/7
Так как число арбузов целое, то единственное значение Х=4 , т.е. фермер продал 4 средних арбуза.
3 + 3 + 4 = 10 (арб). всего арбузов.
ответ: 10 арбузов вырастил фермер.
ответ: 24 км/ч.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила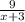
часов и против течения реки, на расстояние в 14 км, лодки затратила 
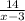часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 
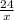часов. Составим уравнение:
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
x₂=24 (км/ч) скорость лодки в стоячей воде.