Зведіть подібні доданки та обчисли значення виразу якщо a=3;b=-2 a) -6a-7b+3a-4b=
b) 1,5a-9b-(a+1,5a)=
v) 0,7-(0,2a-0,3b)+0,2a=

Пусть х часов работала вторая бригада, тогда первая работала 2х часов. 
Производительность труда второй бригады равна 0,8 га/ч, а первой - 0,8х/1,5=8x/15 га/ч. 
Было убрано первой бригадой (8х/15)*2х га, второй - 0,8х га, обеими бригадами вместе (0,8х/15)*2х+0,8х или 12 га.Составим и решим уравнение:
(8х/15)*2х+0,8х=12
16x^2/15+0,8x-12=0    |*15/4
4x^2+3x-45=0
D=3^2-4*4*(-45)=729
x1=(-3+27)/8=3 часа - время работы 2-ой бригады
x2=(-3-27)/8=-3,75<0 (не подходит)
2х=2*3=6 часов - время работы 1-ой бригады
ответ: первая бригада работала 6 часов, а вторая - 3 часа.

Примем за 1 - объем цистерны

Пусть t цис./ч - производительность "медленного" насоса.

Тогда 3t цис./ч - производительность "быстрого" насоса.

(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.

(t+3t)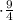 - объем работы системы из двух насосов за 2ч 15мин.

Получим уравнение: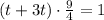

9t = 1

Значит,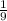 - цис./ч - производительность "медленного" насоса.

Тогда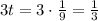 - цис./ч - производительность "быстрого" насоса.

Следовательно,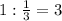 ч - потребуется "быстрому" насосу на заполнение цистерны.

ответ: 3 ч.