1) 9;11;13. 2) 13;11;9.
Объяснение:
Пусть последовательные члены арифметической прогрессии это x,y и z.
Тогда воспользуемся условием и характеристическим свойством арифметической прогрессии ( ) и составим систему уравнений:
Решим квадратное уравнение :
Если x=9, то z=22-9=13;
Если x=13 , то z=22-13=9 .
Тогда получим первые три числа 9; 11 и 13 и вторые 13;11 и 9.
Три числа являются последовательными членами арифметической прогрессии. Сумма их равна 33, а произведение 1287. Найти эти числа.
Запишем условие удобным для решения образом:
первое число из 3-х в арифметической прогрессии
- второе число
- третье число
Значит, их сумма равна:
Зная, что ⇒
А произведение:
Зная, что оно равно 1287 можем составить систему уравнений. Для удобства вычислений заменим на x. Имеем:
(11-d)(11-d+d)(11-d+2d)=1287
(11-d)*11(11+d)=1287
(121-d²)*11=1287
1331-11d²=1287
-11d²=-44
d²=4
d=+-2
Уже ясно, что вариантов ответа будет 2:
Первый вариант:
1) В том случае, если d = 2, имеем:
Имеем: 9; 11; 13
Второй вариант:
2) В том случае, если d = -2, имеем:
Имеем: 13; 11; 9
ответ: 9; 11; 13 и 13; 11; 9
1) 9;11;13. 2) 13;11;9.
Объяснение:
Пусть последовательные члены арифметической прогрессии это x,y и z.
Тогда воспользуемся условием и характеристическим свойством арифметической прогрессии (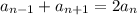
) и составим систему уравнений:
Решим квадратное уравнение :
Если x=9, то z=22-9=13;
Если x=13 , то z=22-13=9 .
Тогда получим первые три числа 9; 11 и 13 и вторые 13;11 и 9.
Три числа являются последовательными членами арифметической прогрессии. Сумма их равна 33, а произведение 1287. Найти эти числа.
Запишем условие удобным для решения образом:
Значит, их сумма равна:
Зная, что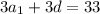
⇒ 
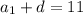
А произведение:
Зная, что оно равно 1287 можем составить систему уравнений. Для удобства вычислений заменим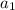
на x. Имеем:
(11-d)(11-d+d)(11-d+2d)=1287
(11-d)*11(11+d)=1287
(121-d²)*11=1287
1331-11d²=1287
-11d²=-44
d²=4
d=+-2
Уже ясно, что вариантов ответа будет 2:
Первый вариант:
1) В том случае, если d = 2, имеем:
Имеем: 9; 11; 13
Второй вариант:
2) В том случае, если d = -2, имеем:
Имеем: 13; 11; 9
ответ: 9; 11; 13 и 13; 11; 9