У якому напрямку плавцеві варто перепливати швидку річку, аби якомога швидше дістатися протилежного берега? Вважайте, що річка має постійну ширину, і плавцю не важливо, до якого саме місця протилежного берега він потрапить​

Объяснение:

– ранець;

– щоденник;

– зошити в клітинку, лінійку – 10 шт; для учнів молодших класів потрібна коса лінія;

– обкладинки для зошитів – 20 шт;

– обкладинки для книг – 1 упаковка;

– папка для зошитів;

– закладки для книг – 1 упаковка;

– підставка для книг;

– ручка – 3-5 шт;

– прості олівці – 2 шт;

– пенал для ручок та олівців;

– стругалка для олівців;

– гумка для стирання олівців;

– 15-сантиметрова лінійка 15-20.

альбом для малювання;

– фарби;

– пензлики;

– кольорові олівці;

– фломастери;

– пластилін;

– дошка для пластиліну.

12.14

Функциональная схема (программа): ,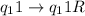

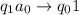
12.17

смотри объяснение

Объяснение:

12.14

Алфавит внутренних состояний Q = {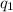, 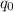} — рабочее состояние и остановка соответственно.

Начальное положение — над первым символом слова.

Будем последовательно считывать символы на ленте, двигаясь по ней слева направо. Если считали 1, просто переходим в соседнюю ячейку:

(R (right) — то же самое, что и П на скриншоте)

Если считали пустой символ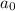 , то мы попали в ячейку сразу после ячейки с последним символом заданного слова. Заменяем этот пустой символ на единицу и останавливаемся:

Построили машину Тьюринга, которая слово вида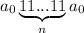 преобразовывает в слово вида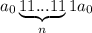

12.17

Внешний алфавит A = {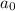, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0} — пустой символ и все цифры десятичной системы счисления.

Алфавит внутренних состояний Q = {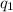, 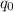} — рабочее состояние и остановка соответственно.

Функциональная схема (программа):

(для i = 1, 2,..., 9)

(L (left) — то же самое, что и Л на скриншоте)

(для i = 1, 2,..., 9)

Начальное положение — над последним символом слова на входе (как написано в тексте на скриншоте, стандартное положение).

Пояснение к работе построенной машины. Если отнимание единицы из последней цифры не требует перехода 10-ти из разряда слева, то просто вычитаем и останавливаемся (первая команда). Но если последняя цифра — ноль, то после замены его на 9 придется перейти к символу слева  (вторая команда) и с ним повторить все те же действия, что и с последним символом. И так до тех пор, пока не встретим символ, отнимание единицы из которого не требует перехода 10-ти из разряда слева. Короче говоря, все как при обычном вычитании в столбик. Последние три команды убирают (заменяют на пустые символы) ведущие нули, если они, конечно, появились.