Средним пропорциональным двух чисел a,b называется такое число с, что
Основные свойства прямоугольного треугольника.
1) Найдем высоту прямоугольного треугольника, применим свойство 1
Гипотенуза прямоугольного треугольника, равна
А теперь найдем катеты a,b, используя свойство 2.
2) Найдем гипотенузу с прямоугольного треугольника, используя свойство 2.
Катет а можно определить по теореме Пифагора:
Найдем высоту h, используя свойство 1.
3) Так как откуда , то, подставляя в свойство 1, получим
По теореме Виетта: — не удовлетворяет условию и
Получили, что гипотенуза прямоугольного треугольника равна 4. Тогда
Используя свойство 1, найдем высоту:
4) Подставим а и c в свойство 2, получим
Высота:
5) Найдем катет bc по теореме Пифагора:
Используя свойство 2, найдем гипотенузу прямоугольного треугольника
6) В условии опечатка видимо, высота не может быть больше чем 3.
7) Применим свойство 1. Найдем ac:
Гипотенуза прямоугольного треугольника:
Найдем катеты a,b применив свойство 2.
8) Применим свойство 1 и найдем катет а и затем катет b
Высота прямоугольного треугольника:
Средним пропорциональным двух чисел a,b называется такое число с, что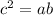
Основные свойства прямоугольного треугольника.
Высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов: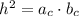
Каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу:1) Найдем высоту прямоугольного треугольника, применим свойство 1
Гипотенуза прямоугольного треугольника, равна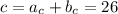
А теперь найдем катеты a,b, используя свойство 2.
2) Найдем гипотенузу с прямоугольного треугольника, используя свойство 2.
Катет а можно определить по теореме Пифагора:
Найдем высоту h, используя свойство 1.
3) Так как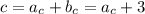 откуда
откуда 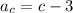 , то, подставляя в свойство 1, получим
, то, подставляя в свойство 1, получим
По теореме Виетта: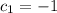 — не удовлетворяет условию и
— не удовлетворяет условию и 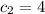
Получили, что гипотенуза прямоугольного треугольника равна 4. Тогда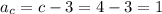
Используя свойство 1, найдем высоту:
4) Подставим а и c в свойство 2, получим
Высота: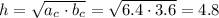
5) Найдем катет bc по теореме Пифагора:
Используя свойство 2, найдем гипотенузу прямоугольного треугольника
6) В условии опечатка видимо, высота не может быть больше чем 3.
7) Применим свойство 1. Найдем ac:
Гипотенуза прямоугольного треугольника: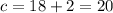
Найдем катеты a,b применив свойство 2.
8) Применим свойство 1 и найдем катет а и затем катет b
Высота прямоугольного треугольника:
Средним пропорциональным двух чисел a,b называется такое число с, что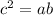
Основные свойства прямоугольного треугольника.
Высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов: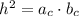
Каждый катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу:1) Найдем высоту прямоугольного треугольника, применим свойство 1
Гипотенуза прямоугольного треугольника, равна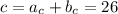
А теперь найдем катеты a,b, используя свойство 2.
2) Найдем гипотенузу с прямоугольного треугольника, используя свойство 2.
Катет а можно определить по теореме Пифагора:
Найдем высоту h, используя свойство 1.
3) Так как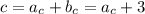 откуда
откуда 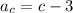 , то, подставляя в свойство 1, получим
, то, подставляя в свойство 1, получим
По теореме Виетта: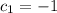 — не удовлетворяет условию и
— не удовлетворяет условию и 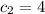
Получили, что гипотенуза прямоугольного треугольника равна 4. Тогда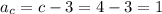
Используя свойство 1, найдем высоту:
4) Подставим а и c в свойство 2, получим
Высота: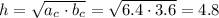
5) Найдем катет bc по теореме Пифагора:
Используя свойство 2, найдем гипотенузу прямоугольного треугольника
6) В условии опечатка видимо, высота не может быть больше чем 3.
7) Применим свойство 1. Найдем ac:
Гипотенуза прямоугольного треугольника: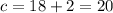
Найдем катеты a,b применив свойство 2.
8) Применим свойство 1 и найдем катет а и затем катет b
Высота прямоугольного треугольника: