1. Длинное плечо рычага равно 6 м, а короткое 2 м Если на длинное плечо подействовать свой 10 H, какой тяжести тело можно
поднять при короткого плеча? (
Оeme: 30Н)
2. При неподвижного блока мальчик поднимает груз
вверх. Если вес мальчика равен 50 кг, определите максимальный вес
груза, который может поднять мальчик при блока? g 10
(Omsem. 500 H). ответ обоснуйте
3. При подъеме тела по наклонной плоскости совершили работу
20 Дж. При этом использовали механизм с КПД, равным so
Найдите полезную рабоry (Orosem l6Дж)
4. Прямоугольное тело имеет длину 6 см, ширину 8 см
Определите расстояние до центра тяжести от любого угла прямо-
угольника?
5. Из колодца поднимают ведро с водой. Обьем ведра 10л.
Радиус вала, на который наматывается трое. 10 см. радиус поворота
рукоятки 50 см. С какой силой нало юдействовать на рукоятку,
чтобы поднять воду? g=10 ответ он)
6. Под действием силы 15 Н rелю поднимают по наклоноіn tnoe-
кости. Найти КПД наклонной плоскости, если ее тела 16 н. высота
наклонной скокти 5 м, длина 64 м. (Ortiser 83,3%).

Показать ответ

Ответ:

charlie911

18.02.2021 17:34

Составим уравнение для пути s за последнюю секунду как разность расстояний, пройденных телом при свободном падении без начальной скорости (υо= 0 ) за время t и за время t - ∆t (по условию ∆t= 1 с): s = gt2/2 - g(t - ∆t)2/2. (1) из этого уравнения находим t : 2s = gt2- g(t - ∆t)2, 2s/g = t2- t2+ 2t∆t - ∆t2 => t = s/g∆t+ ∆t/2. t = 25 м/10 м/с2 ∙1 с + 1/2 с = 3 с. и подставляем его в формулу h = gt2/2. (2) вычислим: h = 10 м/с2∙(3 с)2/2 = 45 м. ответ: 45 м.

0,0(0 оценок)

Ответ:

LAKI2280041

23.12.2021 15:34

300м

Объяснение:

Граф. метод։

У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.

⇒|S(вектор перемещения)| =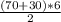 $\frac{(70+30)*6}{2}$ = 300м