1.Мяч бросили вниз, он через 1,6 с упал на землю. На какую высоту был подброшен мяч? 2.Лыжник съезжает с вершины горы с постоянным ускорением а=8,1 м/с^2. Время спуска t=30с, уклон горы а=45. Найдите высоту горы
3. Велосипедист едет по выпуклому мосту. С какой скоростью он должен проходить его середину, чтобы его центростремительное ускорение было равно ускорению свободного падения? (радиус моста R=70м)
4.Какую силу развивает бегущая с ускорением 4,6м/с с калибра, если её масса 5,6 кг
5. С какой силой притягиваются друг другу Солнце и Юпитер, если масса Юпитера mЮ=1900*10^24кг, масса Солнца mС=2*10^30кг, а расстояние между ними r=778,3 *10^6 км
Горизонтальная проекция скорости равна:
Vг = Vo*cosα = 28 * 0,933580426 = 26,14025 м/с
Время полёта находим из уравнения движения в вертикальной плоскости. y = yo+ Vt - gt²/2.
Принимаем g = 10 м/с² и приравниваем нулю (конечная высота).
-5t² + 28t +37 = 0.
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:
D=28^2-4*(-5)*37=784-4*(-5)*37=784-(-4*5)*37=784-(-20)*37=784-(-20*37)=784-(-740)=784+740=1524;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√1524-28)/(2*(-5))=(√1524-28)/(-2*5)=(√1524/10-2.8)=-√1524/10+2.8≈ -1.103844;
t_2=(-√1524-28)/(2*(-5))=(-√1524-28)/(-2*5)=(-√1524-28)/(-10)=-(-√1524-28)/10=-(-√1524/10-28/10)=-(-√1524/10-2.8)=√1524/10+2.8 ≈ 6.7038.
Получаем ответ: L = Vг*t = 26,14025*6.7038 = 175,239 м.
Радиус окружности: R = 20 м.
Пройденный путь: S = L/4.
Найти путь S - ? и модуль перемещения r - ?
А также определить отношение скоростей: <Vп>/<Vr> - ?
Решение:0. Немного фирменных рисунков, смотри приложение.
1. Чтобы найти путь для начала найдём длину окружности. Формула длины окружности: L = 2πR.
2. Путь, пройденный телом - четверть длины окружности: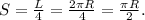
3. Перемещение найдём по теореме Пифагора (см. приложение):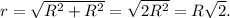
4. Средняя путевая скорость: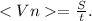
5. Средняя скорость по перемещению: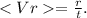
6. Искомое отношение: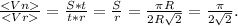
Численно получаем: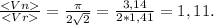
ответ: 31,4 м; 28,3 м; 1,11.