1. Напишите граничные условия для уравнения совместимости перемещений при заданном перемещении граничной поверхности в направлении каждой из координат 2. Напишите граничные условия для уравнения совместимости перемещений при свободных граничных поверхностях
3. Напишите граничные условия для уравнения совместимости перемещений при силовой нагрузке, рспределённой по граничной поверхности
4. Напишите выражения для определения нормальной относительной деформации по перемещениям точек однородной среды
5. Напишите выражения для определения нормальной сдвиговой деформации по перемещениям точек однородной среды
6. Напишите выражения, связывающие нормальные напряжений с перемещениями точек однородной среды
7. Напишите выражения, связывающие сдвиговые напряжения с перемещениями точек однородной среды
Ни в коем случае поверхностное натяжение не зависит от величины поверхности. Оно само есть коэффициент пропорциональности между свободной поверхностной энергией Гиббса и величиной поверхности.
Разумеется, поверхностное натяжение будет изменяться, если в жидкости будут растворены другие вещества, особенно поверхностно-активные (молекулы которых скапливаются в поверхностном слое) . Но введение других веществ в жидкость означает изменение ее природы (была чистая жидкость - стал раствор) .
Для чистой жидкости при определенной температуре поверхностное натяжение - константа, которая приводится в справочниках.
(Это также означает, что поверхностное натяжение жидкости зависит от ее природы и температуры.)
Горизонтальная скорость: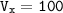 м/с.
м/с.
Высота: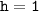 км =
км = 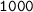 м.
м.
Найти нужно расстояние: - ?
- ?
Решение:1. Разберёмся подробнее, что происходит с грузом. По вертикали груз свободно падает на землю с ускорением свободного падения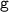 . По горизонтали груз движется равномерно с скоростью
. По горизонтали груз движется равномерно с скоростью 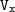 .
.
2. Запишем формулу, определяющую высоту падения: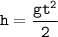 .
.
3. Выразим время падения из (2):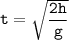 .
.
4. Время падения - время, за которое груз пролетит искомый путь со скоростью
со скоростью 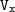 . То есть:
. То есть: 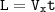 .
.
5. Объединяем (3) и (4):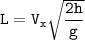 .
.
Численно получим:Переведём в километры: L = 1410 м = 1,41 км.
ответ: 1,41 км.