1) Тело массой 800 г имеет потенциальную энергию 9,6 Дж на любой высоте. будет
(г = 10 Н / кг)
Количество правильных ответов: 2
0,0012 млн
1,2 м
120 см
0,12 см 2) Учащийся весом 2 кг равномерно перемещается на самую высокую точку наклонной плоскости, длиной 5 м и высотой 1 м. При этом сила смещения, параллельная длине наклонной плоскости, составляла 8 Н. Какие результаты должен получить студент при расчете КПД устройства.
Количество правильных ответов: 2
0,5
50%
0,4
5%
40%
3) Вертикально вверх 30 м / с
брошенный на скорости
Кинетика тела массой 100 г
Рассчитайте энергию.
Количество правильных ответов: 2 0,045 кДж 1500Дж 0,45кДж 45кДж 45Дж
1) Для начала мы сделаем рисунок про массивное тело подвешено на невесомой и нерастяжимой нити, чтобы было понятно. (Рисунок сделан внизу).
2) Для начала мы воспользуемся законом сохранения энергий, про этого закона мы найдем максимальную скорость тела:
E(понт.) = E(кин.) - закон сохранения энергий
E(понт.) = mgh - потенциальная энергия
E(кин.) = (m×(υ(max.))²)/2 - кинетическая энергия
Следовательно мы получаем:
mgh = (m×(υ(max.))²)/2 | : m
gh = (υ(max.))²/2 | × 2
2gh = (υ(max.))² ⇒ υ(max.) = √(2gh) - максимальная скорость тела (1)
3) Теперь мы еще в условий сказано что нить с телом отклонили на 60° от вертикали и отпустили - это значит что получится прямоугольный треугольник, потому что нить с телом отклонили на 60° от вертикали и отпустили его вниз. По рисунку мы видим что получился прямоугольный треугольник, но нам надо найти высоту которую тело отпустили, следовательно мы получим:
Пусть гипотенуза нерастяжимой нити - , тогда маленький катет - .
Теперь мы находим высоту, которую указан на рисунке:
- высота которую тело опустили (2)
3) Теперь мы находим общую формулу про максимальную скорость тела пользуясь из (1) и (2), тогда мы получим:
υ(max.) = √(2gh) и h = l/2, следовательно:
υ(max.) = √(2g × (l/2)) = √(g×l) ⇒ υ(max.) = √(g×l) - максимальная скорость тела
Объяснение:
оба стакана должны охладиться до одинаковой температуры (если пренебречь тепловыми потерями), только один из стаканов с водой остывать будет быстрее.
дело в том что теплопередача зависит от разности температур, от коэффициента теплопередачи и от площади теплопередачи.
если мы поделим кубик на 9 частей то его площадь поверхности будет больше чем у кубика разделенного на 6 частей.
значит теплопроводность лучше. значит быстрее остынет тот стакан с водой куда кинули кубик разделенный на 9 частей
Дано:
l = 90 см = 0,9 м
α = 60°
------------------------------
Найти:
υ(max.) - ?
1) Для начала мы сделаем рисунок про массивное тело подвешено на невесомой и нерастяжимой нити, чтобы было понятно. (Рисунок сделан внизу).
2) Для начала мы воспользуемся законом сохранения энергий, про этого закона мы найдем максимальную скорость тела:
E(понт.) = E(кин.) - закон сохранения энергий
E(понт.) = mgh - потенциальная энергия
E(кин.) = (m×(υ(max.))²)/2 - кинетическая энергия
Следовательно мы получаем:
mgh = (m×(υ(max.))²)/2 | : m
gh = (υ(max.))²/2 | × 2
2gh = (υ(max.))² ⇒ υ(max.) = √(2gh) - максимальная скорость тела (1)
3) Теперь мы еще в условий сказано что нить с телом отклонили на 60° от вертикали и отпустили - это значит что получится прямоугольный треугольник, потому что нить с телом отклонили на 60° от вертикали и отпустили его вниз. По рисунку мы видим что получился прямоугольный треугольник, но нам надо найти высоту которую тело отпустили, следовательно мы получим:
Пусть гипотенуза нерастяжимой нити -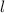
, тогда маленький катет - 
.
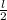Теперь мы находим высоту, которую указан на рисунке:
3) Теперь мы находим общую формулу про максимальную скорость тела пользуясь из (1) и (2), тогда мы получим:
υ(max.) = √(2gh) и h = l/2, следовательно:
υ(max.) = √(2g × (l/2)) = √(g×l) ⇒ υ(max.) = √(g×l) - максимальная скорость тела
υ(max.) = √(9,8 м/с² × 0,9 м) = √(8,82 м²/с²) ≈ 2,97 м/с
ответ: υ(max.) = 2,97 м/с