1) в треугольнике авс аd-биссектриса, угол с равен 30 градусов, угол bad равен 69 градусов. найдите угол adb. ответ дайте в градусах 2)один острый угол прямоугольного треугольника в 87: 8(дробью) раза больше другого. найдите больший острый угол. ответ дайте в градусах 3)в треугольнике abc ас=вс. угол с равен 78 градусов. найдите внешний угол cbd. ответ дайте в градусах. 4) в треугольнике авс ad-биссектриса, угол с равен 45 градусов, угол bad равен 39 градусов. найти угол adb. ответ дайте в градусах.
1) ∠ВАС = 2∠BAD = 2 · 69° = 138°, так как AD биссектриса угла ВАС.
Сумма углов треугольника равна 180°. Из ΔАВС:
∠АВС = 180° - (∠ВАС + ∠АСВ) = 180° - (138° + 30°) = 12°
Из ΔADB:
∠ADB = 180° - (∠BAD + ∠ABD) = 180° - (69° + 12°) = 99°
2) Сумма острых углов прямоугольного треугольника равна 90°.
Пусть ∠1 = х, тогда ∠2 =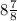 х.
х.
∠1 + ∠2 = 90°
∠2 =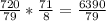
Если же в условии в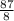 раза больше, то
раза больше, то
∠2 =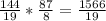
3) Углы при основании равнобедренного треугольника равны:
∠САВ = ∠СВА = (180° - ∠АСВ) / 2 = (180° - 78°) / 2 = 102/2 = 51°
∠CBD = 180° - ∠CBA = 180° - 51° = 129° по свойству смежных углов.
4) ∠ВАС = 2∠BAD = 2 · 39° = 78° так как AD биссектриса.
Сумма углов треугольника равна 180°. Из ΔАВС:
∠АВС = 180° - (∠ВАС + ∠АСВ) = 180° - (78° + 45°) = 180° - 123° = 57°
Из ΔABD:
∠ADB = 180° - (∠ABD + ∠BAD) = 180° - (57° + 39°) = 180° - 96° = 84°