Уравнения, которые заданы видом или , являются уравнениями гармонических колебаний. Здесь — координата колеблющегося тела (смещение от положения равновесия); — амплитуда колебаний; — фаза колебаний; — начальная фаза колебаний.
Скорость движения тела, совершающего гармонические колебания, — первая производная координаты от времени:
Ускорение движения тела, совершающего гармонические колебания, — первая производная скорости от времени, вторая производная координаты от времени:
В нашем уравнении имеем:
Кинетическая энергия — физическая величина, которая характеризует механическое состояние движущегося (колеблющегося) тела и равна половине произведения массы тела на квадрат скорости его движения:
Уравнения, которые заданы видом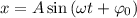 или
или 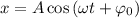 , являются уравнениями гармонических колебаний. Здесь
, являются уравнениями гармонических колебаний. Здесь  — координата колеблющегося тела (смещение от положения равновесия);
— координата колеблющегося тела (смещение от положения равновесия); 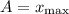 — амплитуда колебаний;
— амплитуда колебаний; 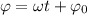 — фаза колебаний;
— фаза колебаний; 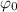 — начальная фаза колебаний.
— начальная фаза колебаний.
Скорость движения тела, совершающего гармонические колебания, — первая производная координаты от времени: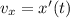
Ускорение движения тела, совершающего гармонические колебания, — первая производная скорости от времени, вторая производная координаты от времени: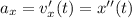
В нашем уравнении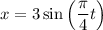 имеем:
имеем:
Кинетическая энергия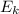 — физическая величина, которая характеризует механическое состояние движущегося (колеблющегося) тела и равна половине произведения массы
— физическая величина, которая характеризует механическое состояние движущегося (колеблющегося) тела и равна половине произведения массы 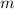 тела на квадрат скорости
тела на квадрат скорости  его движения:
его движения:
Для данной задачи имеем:
c1 = 2100 Дж/кг°с
m2 = 300 г
с2 = 540 Дж/кг°с
t2 = 100°c
t3 = 20°c
t3 - t1 -?
500 г = 0,5 кг
300 г = 0,3 кг
Раз гирька остыла до 20 градусов, значит и керосин нагрелся до 20 градусов, то есть до t3.
Для чугуна имеем:
Q2 = m2×c2×(t3-t2)
Для керосина:
Q1 = m1×c1×(t3-t1)
Уравнение теплового баланса:
Q1 + Q2 = 0
m1×c1×(t3-t1) + m2×c2×(t3-t2) = 0
t3 - t1 = -m2×c2×(t3-t2) / (m1×c1)
t3 - t1 = - 0,3 кг × 540 Дж/кг°с × (20°с - 100°с) / (2100 Дж/кг°с × 0,5 кг) ≈ 12,3°с
ответ: керосин нагрелся примерно на 12,3 градуса. (То есть его начальная температура t1 была около 7,7 градусов)