2. Определить силу взаимодействия двух точечных зарядов Q=Q = 8н Кл, находящихся в вакууме на расстоянии r = 10см. друг от друга. 3. На каком расстоянии друг от друга заряды 1 мкКли 10 нКл TT
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температурыT будет на 273 градуса выше соответствующей температуры t по Цельсию: 100+272 =373 К
Предложим, что давление гелия невелико,тогда начальные условия соответствуют модели идеального газа. Идеальные газы подчиняются уравнению Клапейрона- Менделеева, тогда отсюда получим:
У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
Объяснение:
Дано:
V- 1м3
m-4*10^-3кг
T- 373 К
R- 8,31 Дж/(моль*К)
р -?
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температурыT будет на 273 градуса выше соответствующей температуры t по Цельсию: 100+272 =373 К
Предложим, что давление гелия невелико,тогда начальные условия соответствуют модели идеального газа. Идеальные газы подчиняются уравнению Клапейрона- Менделеева, тогда отсюда получим:
pV=(m/M)RT
из уравнения найдем величину давления гелия:
p=m/M*R/V = (4*10^-3* 8,31 *373)/ 4*10^-3 *1= 3,1*10^3Па
300м
Объяснение:
Граф. метод։
У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
⇒|S(вектор перемещения)| =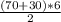
= 300м
Анал. метод։
0) V₀ = 0м/c, V₁ = 6м/c, Δt = 30с
⇒ a₀ = (V₁-V₀)/Δt = 0.2м/c²
⇒ S₀ = a₀Δt²/2 = 90м
1) a₁ = 0м/c²
⇒ S₁ = V₁ × t₁ = 6 × 30 = 180м
2) V₁ = 6м/c V₂ = 0 Δt = 10с
⇒ a₂ = -0.6м/c²
⇒ S₂ = V₁×Δt + a₂Δt²/2 = V₁²/(2×a₂) = 30м
⇒ ∑S = 90 + 180 + 30 = 300м