То есть мы имеем функцию, обратно пропорциональную расстоянию до точечного заряда q.
Есть такое понятие "эквипотенциальные линии", смотри картинку: потенциалы в точках 1 и 3 равны по 1В, а в точке 2 - 4В. И тут надо понимать, на мой взгляд, что условие задачи сформулировано некорректно. Ну посуди: вот середины отрезков 1 и 2, 1 и 3 явно имеют разный потенциал - они не лежат на одной эквипотенциальной окружности, хотя условию и набор 1,2, и набор 1,3 подходят. Так?
Вывод прост: в этой задаче можно рассматривать лишь случай в R1, то есть прямую. И заряд, и 2 точки лежат на одной прямой.
1) Найдем начальную высоту тела:
Eп₀ = mgh₀; 20 Дж = 2 кг * 10 м/с² * h₀; h₀ = 1 м.
2) В момент максимального подъема тела его скорость стала равна 0. Найдем время движения тела вверх:
υ = υ₀ - gt = 4 м/с - 10 м/с² * t = 0; t =0,4 с.
2) Найдем, на какую высоту поднялось тело:
S = x₀ + υ₀t - gt²/2 = 1 м + 4 м/с * 0,4 с - (10 м/с² * 0,4² с²) / 2 = 1 м + 1,6 м - 5 * 0,16 м = 2,6 м - 0,8 м = 1,8 м.
3) Потенциальная энергия тела на максимальной высоте стала равной
Eп = mgh = 2 кг * 10 м/с² * 1,8 м = 36 Дж;
4) Согласно закону превращения механической энергии в момент падения тела потенциальная энергия превратилась в кинетическую.
Eк = 36 Дж.
Eк = mυ²/2; υ² = 2*Eк /m; υ² = 2*36 Дж / 2 кг = 36 м/с;
υ = 6 м/с.
1,6B
Объяснение:
Для поля точечного заряда потенциал равен:
φ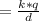
То есть мы имеем функцию, обратно пропорциональную расстоянию до точечного заряда q.
Есть такое понятие "эквипотенциальные линии", смотри картинку: потенциалы в точках 1 и 3 равны по 1В, а в точке 2 - 4В. И тут надо понимать, на мой взгляд, что условие задачи сформулировано некорректно. Ну посуди: вот середины отрезков 1 и 2, 1 и 3 явно имеют разный потенциал - они не лежат на одной эквипотенциальной окружности, хотя условию и набор 1,2, и набор 1,3 подходят. Так?
Вывод прост: в этой задаче можно рассматривать лишь случай в R1, то есть прямую. И заряд, и 2 точки лежат на одной прямой.
Тогда искомый потенциал:
φ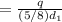 =1,6B
=1,6B