4 5(2) Під час набирання скляні палички об клаптик шовкової тканиниили набуває позитивного заряду. Які ми спі, терігаються з деякими атомами, які розташовані на поверхні палички?
Сила , возникающая в результате деформации тела и направления в сторону , противоположную перемещениям частиц тела при этой деформации , называется силой упругости . Опыты со стержнем показатели , что при малых по сравнению с размерами тела деформации модуль силы упругости прямо пропорционален модулю вектора перемещения свободного конца стержня , что в проекции проглядеть как Эту связь установил Р.Гук , его закон формируется так сила упругости возникающая при деформации тела пропорциональна удлинение тела
Пусть рассматривается движение двух шаров под номерами 1 и 2. Выберем такую систему отсчета, в которой скорость второго шарика равна нулю. Пусть также - векторы скоростей первого шарика до и после столкновения соответственно. Точно также определим ; Понятно, что удар нецентральный, иначе никакого угла и не было бы. Запишем закон сохранения импульса, с учетом ("масса" сократится): ; Теперь возведем обе части в квадрат: ; Теперь запишем закон сохранения энергии (сократив на массу):
; Сравнивая полученные выражения, приходим к выводу, что , что в общем-то и требовалось
Сила , возникающая в результате деформации тела и направления в сторону , противоположную перемещениям частиц тела при этой деформации , называется силой упругости . Опыты со стержнем показатели , что при малых по сравнению с размерами тела деформации модуль силы упругости прямо пропорционален модулю вектора перемещения свободного конца стержня , что в проекции проглядеть как Эту связь установил Р.Гук , его закон формируется так сила упругости возникающая при деформации тела пропорциональна удлинение тела
Пусть рассматривается движение двух шаров под номерами 1 и 2. Выберем такую систему отсчета, в которой скорость второго шарика равна нулю. Пусть также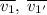 - векторы скоростей первого шарика до и после столкновения соответственно. Точно также определим
- векторы скоростей первого шарика до и после столкновения соответственно. Точно также определим 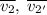 ; Понятно, что удар нецентральный, иначе никакого угла и не было бы. Запишем закон сохранения импульса, с учетом
; Понятно, что удар нецентральный, иначе никакого угла и не было бы. Запишем закон сохранения импульса, с учетом 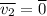 ("масса" сократится):
("масса" сократится): 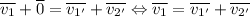 ; Теперь возведем обе части в квадрат:
; Теперь возведем обе части в квадрат: 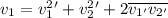 ; Теперь запишем закон сохранения энергии (сократив на массу):
; Теперь запишем закон сохранения энергии (сократив на массу):