4)Маленькая лампочка размещается на 1,41 м от поверхности стола. Освещенность в той точке стола, куда свет падает перпендикулярно, составляет 100 лк. Объясните, как изменится освещение в той точке стола, где свет падает перпендикулярно, если лампочку поставить в 2 раза ближе! 5)Если положить на стол лист белой бумаги, поток падающего на него света составляет 4 люмена, а освещенность поверхности – 100 лк. Предположим, что свет падает перпендикулярно поверхности листа и его поток равномерно распределяется по всей поверхности листа. Запишите, какое соотношение (формулу) следует использовать для определения площади поверхности листа!

R₁ = 259.8 H;   R₂ = 150 H

Объяснение:

Будем считать, угол между левой и правой опорными плоскостями равен 90°.

G = 300H

R₁ - ? - реакция правой опорной плоскости (направлена перпендикулярно этой плоскости по её внешней нормали)

R₂ - ? - реакция левой опорной плоскости (направлена перпендикулярно этой плоскости по её внешней нормали)

Очевидно, что R₁ ⊥ R₂

Проецируем систему сил на направление R₁

R₁ - G · cos 30° = 0

R₁  =  G · cos 30° = 300 · 0.866 = 259.8 (H)

Проецируем систему сил на направление R₂

R₂ - G · sin 30° = 0

R₂  =  G · sin 30° = 300 · 0.5 = 150 (H)

11,25 м

Объяснение:

Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:

Откуда:

Горизонтальная составляющая скорости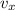 будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):

м/с

Искомый радиус кривизны траектории:

м.