5. Скільки гасу треба спалити, щоб 3 кг льоду, взятого за температури -20 градусів Цельсія , Випарувати при температурі кипіння?​

Объяснение:

Начнем с того, что кинетическая энергия находится по формуле

Eк =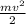

Из этой формулы нам надо выразить квадрат скорости. Но для начала мы Eк домножим на два.

Получим уравнение:

2Eк = mv^2 (^2 - степень числа)

Выразим из этого уравнения квадрат скорости.

v^2 =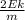

Подставим величины в формулу:

v^2 =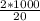

v^2 = 100

А теперь вопрос: вы хоть раз слышали что-то о квадратных корнях?

Так вот, квадратные корни вы будете проходить по алгебре в 8 классе.  Извлечение квадратного корня(в нашем случае - арифметического) - это такое неотрицательное число, которое в нашем случае при возведении в квадрат даст 100.

То есть,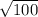 = 10 м/с

То есть, скорость тела равна 10 м/с.

Задача решена.

Объяснение:

Дано:

m₁ = 19,7·10⁻³ кг

t₁ = 100⁰C;  

m₂ = 0,35 кг

с₂ = 4200 Дж/(кг·°С)

T₂ = 281 K;    t₂ = 281-273 = 8⁰C

m₃ = 0,2 кг

t₃ = 8⁰C

L = 22,6·10⁵ Дж/кг

T = 313 К;   t = 313 - 273 = 40⁰ C

с₃ - ?

1)

Пар конденсируется:

Q₁ = L·m₁ = 22,6·10⁵·19,7·10⁻³ ≈ 44 500 Дж

2)

Вода, получившаяся из пара, остывает:

Q₁₂ = c₂·m₁·(100 - t) = 4200·19,7·10⁻³·(100-40) ≈ 5 000 Дж

3)

Холодная вода нагревается:

Q₂ = c₂·m₂·(t - t₂) =  4200·0,35·(40-8) ≈ 47  000  Дж

4)

Нагревается и калориметр:

Q₃ = c₃·m₃·(t - t₃) = c₃·0,2·(40-8) =6,4·c₃  Дж

5)

Составим уравнение теплового баланса:

Q₁ +Q₁₂= Q₂ + Q₃

44 500 + 5 000 = 47 000 + 6,4·c₃

6,4·c₃ = 44 500 + 5 000 - 47 000

6,4·c₃ = 2500

c₃ = 2 500 / 6,4 ≈ 390 Дж/(кг·°С)

Калориметр изготовлен из меди (но, может быть из латуни или цинка, для которых с₃ = 380 Дж/(кг·°С)